Dance of the Errors
One of the big problems that has come up in recent years is in how to represent the uncertainty in certain estimates. Astronomers usually present errors as +-stddev on the quantities of interest, but that presupposes that the errors are uncorrelated. But suppose you are estimating a multi-dimensional set of parameters that may have large correlations amongst themselves? One such case is that of Differential Emission Measures (DEM), where the “quantity of emission” from a plasma (loosely, how much stuff there is available to emit — it is the product of the volume and the densities of electrons and H) is estimated for different temperatures. See the plots at the PoA DEM tutorial for examples of how we are currently trying to visualize the error bars. Another example is the correlated systematic uncertainties in effective areas (Drake et al., 2005, Chandra Cal Workshop). This is not dissimilar to the problem of determining the significance of a “feature” in an image (Connors, A. & van Dyk, D.A., 2007, SCMA IV).
Here is a specific example that came up due to a comment by a referee on a paper with David G.-A. We had said that the O abundance is dominated by uncertainties in the DEM at low temperatures because that is where most of the emission from O is formed. The referee disputed this, saying yeah, but O is also present at higher temperatures, and since the DEM is much higher there, that should be the predominant contribution to the estimate. In effect, the referee said, “show me!” The problem is, how? The measured fluxes are:
fO7obs = 2 +- 0.75
fO8obs = 4 +- 0.88
The predicted fluxes are:
fO7pred = 1.8 +- 0.72
fO8pred = 3.6 +- 0.96
where the error bars here come from the stddev of the fluxes predicted by each DEM realization that comes out of the MCMC analysis. On the face of it, it looks like a pretty good match to the observations, though a slightly different picture emerges if one were to look at the distribution of the predicted fluxes:
mode(fO7pred)=0.76 (95% HPD interval = 0.025:2.44)
mode(fO8pred)=2.15 (95% HPD interval = 0.95:4.59)
What if one computed the flux at each temperature and did the same calculation separately? That is shown in the following plot, where the product of the DEM and the line emissivity computed at each temperature bin is shown for both O VII (red) and O VIII (blue). The histograms are for the best-fit DEM solution, and the vertical bars are stddevs on the product, which differs from the flux only by a constant. The dashed lines show the 95% highest posterior density intervals.

Figure 1: Fluxes from O VII and O VIII computed at each temperature from DEM solution of RST 137B. The solid histograms are the fluxes for the best-fit DEM, and the vertical bars are the stddev for each temperature bin. The dotted lines denote the 95% highest-posterior density intervals for each temperature.
But even this tells an incomplete tale. The full measure of the uncertainty goes unseen until all the individual curves are seen, as in the animated gif below which shows the flux calculated for each MCMC draw of the DEM:
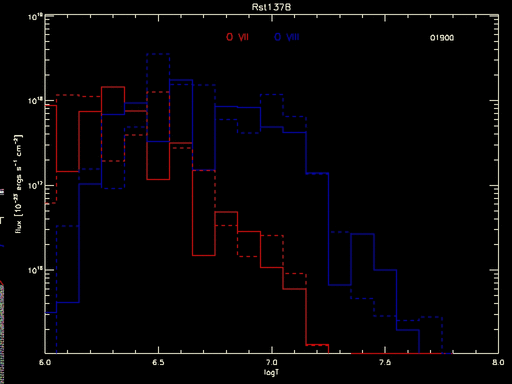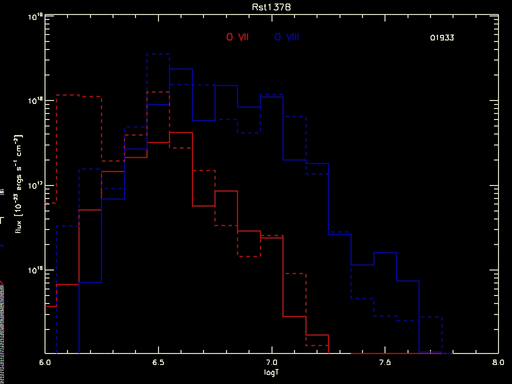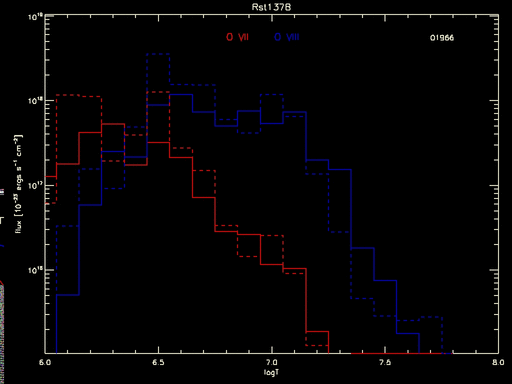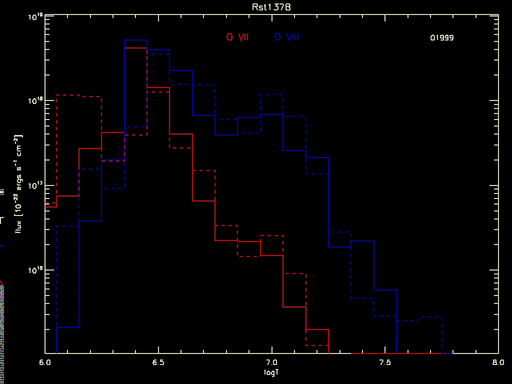
Figure 2: Predicted flux in O VII and O VIII lines as a product of line emissivity and MCMC samples of the DEM for various temperatures. The dashed histogram is from the best-fit DEM, the solid histograms are for the various samples (the running number at top right indicates the sample sequence; only the last 100 of the 2000 MCMC draws are shown).
So this brings me to my question. How does one represent this kind of uncertainty in a static plot? We know what the uncertainty is, we just don’t know how to publish them.
hlee:
A naive question, here since I don’t understand the process. What is the time related variable in the animation? Or is it realization of multiple simulations? I wonder if the point is that conditioning (temperature) affects and want to find a way of including the model uncertainty in the final estimates.
01-26-2008, 6:57 pmvlk:
Ah, it appears that the figure captions don’t show up when you mouse over, as I had expected they would. I have now added the captions explicitly in the text.
The short answer is, there is no time dependence — these are fluxes calculated from the MCMC draws of the DEMs. MCMC is used to draw the parameters that determine the DEM as a function of temperature, which in turn is used to calculate the intensity in each temperature bin.
i.e., these are the model uncertainties. And the point is that the uncertainty structure is far richer than is usually represented, as e.g., in the third set of equations above, and even the graphical representation of Figure 1 is insufficient to capture the correlations and magnitudes across both temperatures and lines.
01-26-2008, 10:46 pm