

Next: This Work
Previous: Rotation
Periods of ZAMS Stars
The core--envelope decoupling model was developed out
of a desire to reproduce the observed period
distribution at 50-500 Myrs of age.
Another way to approach this problem is to observe the youngest stars,
from < 1 to about 10 Myrs, and try to see how the UFRs
are formed.
There are currently several groups involved in the studies of the
rotation periods of PMS stars. The Van Vleck Observatory
(cf. Attridge and Herbst 1992) has concentrated on single band photometry
of the Orion Nebula Cluster (ONC) where the stars are expected to be
less than a million years old (Brown 1996). Prosser et al.
(1993a, 1993b, 1995)
have concentrated their work on the somewhat older 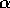 Persei and
Pleiades clusters, but have monitored a few TTs. Grankin (1993, 1994)
and the COYOTES group (Bouvier et al. 1993, 1995)
have been primarily concerned with rotation periods of classical T Tauri
stars (cTTs), (and to a lesser extent nTTs) in the Taurus--Auriga
association.
Persei and
Pleiades clusters, but have monitored a few TTs. Grankin (1993, 1994)
and the COYOTES group (Bouvier et al. 1993, 1995)
have been primarily concerned with rotation periods of classical T Tauri
stars (cTTs), (and to a lesser extent nTTs) in the Taurus--Auriga
association.
These works individually focus on specific clusters at specific stages
in formation, but taken as a whole they have begun to clarify the
evolution of angular momentum in young stars. Overall, there are
about 100 rotation periods known for PMS stars.
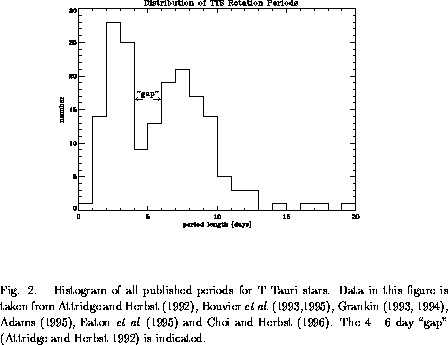
Figure 2 shows a
summary of the bulk of the published results. The main feature of the
figure is the bimodal distribution of the periods. Peaks in the
distribution occur near 8 days and 3 days.
Furthermore, the stars with periods near 8 days also tend to
have infrared excesses which can be interpreted as arising from disks.
The distribution is clearly bimodal; there are 20 stars in the
``gap'' from 4 to 6 days which is about half the number expected for a
smooth distribution.
This bimodal distribution can be thought of in
two physically distinct ways. The gap may arise either because the
distribution has a hole, or because it is made up of two distinct
distributions. In the first interpretation,
the gap occurs because locking mechanism holds
stars at a 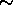 eight day rotation period. Once the lock is broken,
the star is free to spin--up. The stars quickly increase their
rotational period. The pile--up observed in the faster peak is the
result of probable internal breaking and binning effects.
If this is the case, the depth and width of the gap is a function of
how fast stars spin up after they lose their disk and how quickly such
spin up is halted.
The latter interpretation assumes that PMS stars naturally bifurcate
into two types, fast rotators and slow rotators. In this case, the
dearth of stars from four to six days is a manifestation of the
lack of strength in the wings of the two distribution. There are no
no evolutionary parameters which can
be derived from the depth of the gap.
eight day rotation period. Once the lock is broken,
the star is free to spin--up. The stars quickly increase their
rotational period. The pile--up observed in the faster peak is the
result of probable internal breaking and binning effects.
If this is the case, the depth and width of the gap is a function of
how fast stars spin up after they lose their disk and how quickly such
spin up is halted.
The latter interpretation assumes that PMS stars naturally bifurcate
into two types, fast rotators and slow rotators. In this case, the
dearth of stars from four to six days is a manifestation of the
lack of strength in the wings of the two distribution. There are no
no evolutionary parameters which can
be derived from the depth of the gap.
Edwards et al. (1993) were the first to suggest
that the peak in the distribution
near eight days is evidence for disk locking. In a cTTs system with
an optically
thick disk, the star may be magnetically coupled to the disk. Any
tendency of the star's rotation period to decrease as the star contracts
is mitigated by drag on the stellar magnetic field by the disk.
This holds rotation periods at about eight days.
Once the disk has dissipated, the star is free to spin--up.
At this point the rotation rate of
the star quickly increases until its peak rotation rate is reached.
This appears to be less than three days for many stars.
Königl (1991) showed that if the magnetic field truncated at the inner
edge of the accretion disk, the drag of charged particles in the disk
on the stellar magnetic field could slow the rotation of the star.
Cameron et al. (1994) modeled one such mechanism and
found that for a cTTs with a magnetic field strength of a few
hundred gauss, the torque of the disk on the star could slow the
star's rotation into a quasi--static equilibrium. Further, they found that
that the effect is nearly independent of stellar mass and also
independent of disk mass above a critical value.
Shu et al. (1994) included a similar mechanism into their
magnetocentrifugally driven ``X--celerator wind'' model. They show that a
long (eight day) rotation period is a natural consequence of
accretion through a magnetically
truncated disk using their X-celerator wind.



Next: This Work
Up: No Title
Previous: Rotation Periods of
Scott J. Wolk
Wed Dec 4 18:01:50 EST 1996
 Persei and
Pleiades clusters, but have monitored a few TTs. Grankin (1993, 1994)
and the COYOTES group (Bouvier et al. 1993, 1995)
have been primarily concerned with rotation periods of classical T Tauri
stars (cTTs), (and to a lesser extent nTTs) in the Taurus--Auriga
association.
Persei and
Pleiades clusters, but have monitored a few TTs. Grankin (1993, 1994)
and the COYOTES group (Bouvier et al. 1993, 1995)
have been primarily concerned with rotation periods of classical T Tauri
stars (cTTs), (and to a lesser extent nTTs) in the Taurus--Auriga
association.
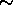 eight day rotation period. Once the lock is broken,
the star is free to spin--up. The stars quickly increase their
rotational period. The pile--up observed in the faster peak is the
result of probable internal breaking and binning effects.
If this is the case, the depth and width of the gap is a function of
how fast stars spin up after they lose their disk and how quickly such
spin up is halted.
The latter interpretation assumes that PMS stars naturally bifurcate
into two types, fast rotators and slow rotators. In this case, the
dearth of stars from four to six days is a manifestation of the
lack of strength in the wings of the two distribution. There are no
no evolutionary parameters which can
be derived from the depth of the gap.
eight day rotation period. Once the lock is broken,
the star is free to spin--up. The stars quickly increase their
rotational period. The pile--up observed in the faster peak is the
result of probable internal breaking and binning effects.
If this is the case, the depth and width of the gap is a function of
how fast stars spin up after they lose their disk and how quickly such
spin up is halted.
The latter interpretation assumes that PMS stars naturally bifurcate
into two types, fast rotators and slow rotators. In this case, the
dearth of stars from four to six days is a manifestation of the
lack of strength in the wings of the two distribution. There are no
no evolutionary parameters which can
be derived from the depth of the gap.
