


Next: X--ray Activity and
PMS stars
Introduction
Since the beginning of the twentieth century, one of the most
perplexing problems
in our understanding of the development of the Solar System, and stars
in general, has been the disposition of angular momentum. It is the
only significant observable quantity in the Solar System that the Sun
does not dominate. In the early 1970s, it was shown that for stars of
mass 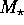 > 1.5 M
> 1.5 M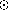 , their specific angular momenta fall on
the relation
, their specific angular momenta fall on
the relation  , where
, where
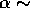 2/3 and J
is the specific angular momentum. While the Sun itself and similar
low--mass stars fall below this relation by two orders of magnitude,
the Solar System as a whole fits this relation (Kraft 1970).
This observation was consistent
with the independently derived theoretical result that an accretion
disk provided a simple mechanism
for allowing mass to collect on a central object while controlling the
growth of angular momentum (Lynden--Bell and Pringle 1972).
2/3 and J
is the specific angular momentum. While the Sun itself and similar
low--mass stars fall below this relation by two orders of magnitude,
the Solar System as a whole fits this relation (Kraft 1970).
This observation was consistent
with the independently derived theoretical result that an accretion
disk provided a simple mechanism
for allowing mass to collect on a central object while controlling the
growth of angular momentum (Lynden--Bell and Pringle 1972).
Over the past two decades, the existence of such accretion disks has
been clearly demonstrated. As a star forms, not only is
its own angular momentum being determined, but also the angular
momentum available for
its planetary system. This has made the need to study the evolution of
the rotation periods of stars, and hence the angular momentum, very clear.
The study of rotation gives us insight into the physical processes inside
stars. In the case of low mass pre--main sequence (PMS) stars, we seek to
learn whether disks alone determine the angular momentum distribution when
stars arrive on the main sequence. It is also likely that
the angular momentum loss mechanism varies as the star evolves.
The basics of the evolution of the rotation of a star with fixed angular
momentum are fairly straightforward.
Assuming that there is no significant loss of angular momentum during a
star's evolution following the Hayashi track, spin--up is a result of
conservation of angular momentum as the stellar radius decreases.
Under these conditions, angular momentum (J)
is constant (typically 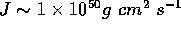 ; here I am going to be primarily
concerned with the magnitude of J and not its vector nature).
Since
; here I am going to be primarily
concerned with the magnitude of J and not its vector nature).
Since 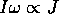 and
and 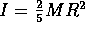 (for the simple case of a uniform density distribution),
as R goes down by a factor of 10,
(for the simple case of a uniform density distribution),
as R goes down by a factor of 10,  must go up by a factor of
100. Further, since
must go up by a factor of
100. Further, since 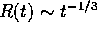 , then
, then 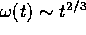 .
. After stars have attained their main--sequence radii, they
continue to spin--up as more material settles toward the center of the
star. Once stars have achieved their stable main--sequence
configurations, they
will spin--down appreciably during the main sequence lifetime
(Skumanich 1972). This is
because they will continually lose angular momenta to the stellar
wind as shown by Endal & Sofia (1981).
After stars have attained their main--sequence radii, they
continue to spin--up as more material settles toward the center of the
star. Once stars have achieved their stable main--sequence
configurations, they
will spin--down appreciably during the main sequence lifetime
(Skumanich 1972). This is
because they will continually lose angular momenta to the stellar
wind as shown by Endal & Sofia (1981).
If one assumes that angular momentum is conserved
from the natal cloud, then rotation periods exceeding breakup velocity are
implied for
PMS stars. This conclusion was supported by the earliest measurements of
 for PMS stars (Herbig 1957). However this work was on
atypical stars including SU Aurigæ. The first systematic
study of the rotational periods of PMS stars was undertaken by
Vogel & Kuhi (1981). They studied the rotational velocities of a
large sample of stars in the Taurus--Auriga star forming region.
They found, for the most part, that there were no rapid rotators among
(classical) T Tauri stars. Hartmann et al.
(1986) and Bouvier et al. (1986) reached similar results, finding the
mean rotational velocity for T Tauri stars (TTs) was about 15 km/s or
about 10%
of the breakup velocity. These results were
surprising, not only for the theoretical reasons just described,
but also because main sequence stars show a correlation between
activity and rotation period (Noyes et al. 1984). PMS stars are highly
active, yet the rotation velocities do not seem well correlated.
Evidently, while
rotation and
activity are linked in main sequence stars, PMS stars either have a
non--dynamo activity source, or other mitigating factors, which
disconnect the observed activity from the rotational velocity.
for PMS stars (Herbig 1957). However this work was on
atypical stars including SU Aurigæ. The first systematic
study of the rotational periods of PMS stars was undertaken by
Vogel & Kuhi (1981). They studied the rotational velocities of a
large sample of stars in the Taurus--Auriga star forming region.
They found, for the most part, that there were no rapid rotators among
(classical) T Tauri stars. Hartmann et al.
(1986) and Bouvier et al. (1986) reached similar results, finding the
mean rotational velocity for T Tauri stars (TTs) was about 15 km/s or
about 10%
of the breakup velocity. These results were
surprising, not only for the theoretical reasons just described,
but also because main sequence stars show a correlation between
activity and rotation period (Noyes et al. 1984). PMS stars are highly
active, yet the rotation velocities do not seem well correlated.
Evidently, while
rotation and
activity are linked in main sequence stars, PMS stars either have a
non--dynamo activity source, or other mitigating factors, which
disconnect the observed activity from the rotational velocity.



Next: X--ray Activity and
Scott J. Wolk
Wed Dec 4 18:01:50 EST 1996
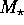 > 1.5 M
> 1.5 M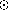 , their specific angular momenta fall on
the relation
, their specific angular momenta fall on
the relation  , where
, where
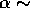 2/3 and J
is the specific angular momentum. While the Sun itself and similar
low--mass stars fall below this relation by two orders of magnitude,
the Solar System as a whole fits this relation (Kraft 1970).
This observation was consistent
with the independently derived theoretical result that an accretion
disk provided a simple mechanism
for allowing mass to collect on a central object while controlling the
growth of angular momentum (Lynden--Bell and Pringle 1972).
2/3 and J
is the specific angular momentum. While the Sun itself and similar
low--mass stars fall below this relation by two orders of magnitude,
the Solar System as a whole fits this relation (Kraft 1970).
This observation was consistent
with the independently derived theoretical result that an accretion
disk provided a simple mechanism
for allowing mass to collect on a central object while controlling the
growth of angular momentum (Lynden--Bell and Pringle 1972).
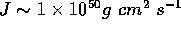 ; here I am going to be primarily
concerned with the magnitude of J and not its vector nature).
Since
; here I am going to be primarily
concerned with the magnitude of J and not its vector nature).
Since 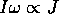 and
and 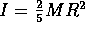 (for the simple case of a uniform density distribution),
as R goes down by a factor of 10,
(for the simple case of a uniform density distribution),
as R goes down by a factor of 10,  must go up by a factor of
100. Further, since
must go up by a factor of
100. Further, since 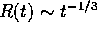 , then
, then 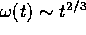 .
. for PMS stars (Herbig 1957). However this work was on
atypical stars including SU Aurigæ. The first systematic
study of the rotational periods of PMS stars was undertaken by
Vogel & Kuhi (1981). They studied the rotational velocities of a
large sample of stars in the Taurus--Auriga star forming region.
They found, for the most part, that there were no rapid rotators among
(classical) T Tauri stars. Hartmann et al.
(1986) and Bouvier et al. (1986) reached similar results, finding the
mean rotational velocity for T Tauri stars (TTs) was about 15 km/s or
about 10%
of the breakup velocity. These results were
surprising, not only for the theoretical reasons just described,
but also because main sequence stars show a correlation between
activity and rotation period (Noyes et al. 1984). PMS stars are highly
active, yet the rotation velocities do not seem well correlated.
Evidently, while
rotation and
activity are linked in main sequence stars, PMS stars either have a
non--dynamo activity source, or other mitigating factors, which
disconnect the observed activity from the rotational velocity.
for PMS stars (Herbig 1957). However this work was on
atypical stars including SU Aurigæ. The first systematic
study of the rotational periods of PMS stars was undertaken by
Vogel & Kuhi (1981). They studied the rotational velocities of a
large sample of stars in the Taurus--Auriga star forming region.
They found, for the most part, that there were no rapid rotators among
(classical) T Tauri stars. Hartmann et al.
(1986) and Bouvier et al. (1986) reached similar results, finding the
mean rotational velocity for T Tauri stars (TTs) was about 15 km/s or
about 10%
of the breakup velocity. These results were
surprising, not only for the theoretical reasons just described,
but also because main sequence stars show a correlation between
activity and rotation period (Noyes et al. 1984). PMS stars are highly
active, yet the rotation velocities do not seem well correlated.
Evidently, while
rotation and
activity are linked in main sequence stars, PMS stars either have a
non--dynamo activity source, or other mitigating factors, which
disconnect the observed activity from the rotational velocity.