Sersic2D

class astropy.modeling.functional_models.Sersic2D(amplitude=1, r_eff=1, n=4, x_0=0, y_0=0, ellip=0, theta=0, **kwargs)

Bases: astropy.modeling.Fittable2DModel

Two dimensional Sersic surface brightness profile.

Parameters:

amplitude : float

Surface brightness at r_eff.

r_eff : float

Effective (half-light) radius

n : float

Sersic Index.

x_0 : float, optional

x position of the center.

y_0 : float, optional

y position of the center.

ellip : float, optional

Ellipticity.

theta : float, optional

Rotation angle in radians, counterclockwise from the positive x-axis.

Other Parameters:  

fixed : a dict, optional

A dictionary {parameter_name: boolean} of parameters to not be varied during fitting. True means the parameter is held fixed. Alternatively the fixed property of a parameter may be used.

tied : dict, optional

A dictionary {parameter_name: callable} of parameters which are linked to some other parameter. The dictionary values are callables providing the linking relationship. Alternatively the tied property of a parameter may be used.

bounds : dict, optional

A dictionary {parameter_name: value} of lower and upper bounds of parameters. Keys are parameter names. Values are a list or a tuple of length 2 giving the desired range for the parameter. Alternatively, the min and max properties of a parameter may be used.

eqcons : list, optional

A list of functions of length n such that eqcons[j](x0,*args) == 0.0 in a successfully optimized problem.

ineqcons : list, optional

A list of functions of length n such that ieqcons[j](x0,*args) >= 0.0 is a successfully optimized problem.

See also

Gaussian2D, Moffat2D

Notes

Model formula:

\[I(x,y) = I(r) = I_e\exp\left\{-b_n\left[\left(\frac{r}{r_{e}}\right)^{(1/n)}-1\right]\right\}\]

The constant \(b_n\) is defined such that \(r_e\) contains half the total luminosity, and can be solved for numerically.

\[\Gamma(2n) = 2\gamma (b_n,2n)\]

References

[1]	http://ned.ipac.caltech.edu/level5/March05/Graham/Graham2.html

Examples

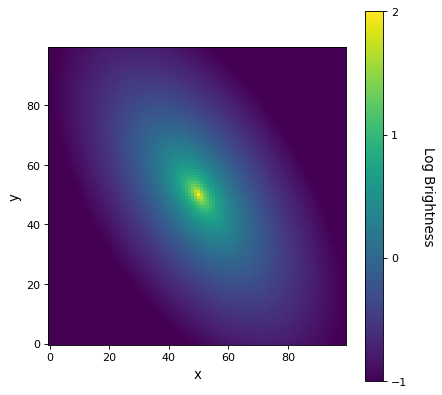
import numpy as np
from astropy.modeling.models import Sersic2D
import matplotlib.pyplot as plt

x,y = np.meshgrid(np.arange(100), np.arange(100))

mod = Sersic2D(amplitude = 1, r_eff = 25, n=4, x_0=50, y_0=50,
               ellip=.5, theta=-1)
img = mod(x, y)
log_img = np.log10(img)

plt.figure()
plt.imshow(log_img, origin='lower', interpolation='nearest',
           vmin=-1, vmax=2)
plt.xlabel('x')
plt.ylabel('y')
cbar = plt.colorbar()
cbar.set_label('Log Brightness', rotation=270, labelpad=25)
cbar.set_ticks([-1, 0, 1, 2], update_ticks=True)
plt.show()

(png, svg, pdf)

Attributes Summary

amplitude
ellip
input_units	This property is used to indicate what units or sets of units the evaluate method expects, and returns a dictionary mapping inputs to units (or None if any units are accepted).
n
param_names
r_eff
theta
x_0
y_0

Methods Summary

evaluate(x, y, amplitude, r_eff, n, x_0, …)

Two dimensional Sersic profile function.

Attributes Documentation

amplitude = Parameter('amplitude', value=1.0)

ellip = Parameter('ellip', value=0.0)

input_units

This property is used to indicate what units or sets of units the evaluate method expects, and returns a dictionary mapping inputs to units (or None if any units are accepted).

Model sub-classes can also use function annotations in evaluate to indicate valid input units, in which case this property should not be overridden since it will return the input units based on the annotations.

n = Parameter('n', value=4.0)

param_names = ('amplitude', 'r_eff', 'n', 'x_0', 'y_0', 'ellip', 'theta')

r_eff = Parameter('r_eff', value=1.0)

theta = Parameter('theta', value=0.0)

x_0 = Parameter('x_0', value=0.0)

y_0 = Parameter('y_0', value=0.0)

Methods Documentation

classmethod evaluate(x, y, amplitude, r_eff, n, x_0, y_0, ellip, theta)

Two dimensional Sersic profile function.