


Next: Simulations
Up: Period Determination
Previous: False Alarms and
The term ``spectral window'' is used to describe the response of the data
analysis system to a perfect sine wave.
If one observes a non-variable object with finite signal--to--noise
each night at exactly the
same time (equivalently an object with a one day period), the
periodogram analysis on it will return a
power spectrum that is peaked at 1 day. This means that there is
a periodic signature from the sampling frequency itself.
The observing times define a
window. This window, convolved with the signal, determines the
periodogram (Deeming 1975). The sampling frequency
enters because you can define a period that is not the true period,
yet hits all the observed points.
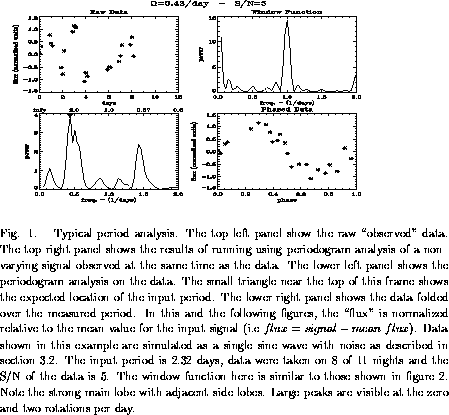
Figure 1 shows a typical analysis, including the window
function. This demonstrates the main features of the window function. First
there is a narrow central peak with width 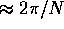 where N
equals the number of samples. The number of samples taken
places a fundamental limit on the accuracy of the period measurement.
Second, there are roughly evenly spaced side lobes.
These side lobes contain spectral leakage due to high frequency
components in the Fourier transform of the original signal.
Third, the total power in the peak of the window function is greater
than the power of the true signal by a factor of a few.
Finally, there are large peaks on either side of the main lobe displace by one
rotation per day. This is due to the one day periodicity in the
observations. The windowing can
cause a problem with period determination since periods very close to
one day and very long periods and appear similar to the null signal
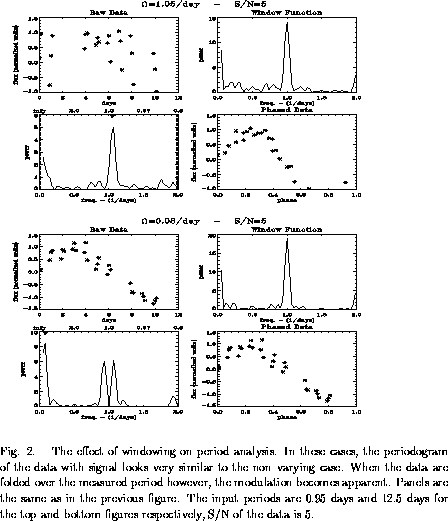
case. Careful study of Figure 2 reveals difference
between the window function and periodograms of these signals. Even
with only 30 samples, periods deviating from a day by 1% are detectable.
For convincing results though, the periodogram requires
the aid of other data analysis. This usually consists of visual
inspection of the raw data and the phased data. To gain a better
understanding of how the observational data behave, simulations were
run using synthetic data.
where N
equals the number of samples. The number of samples taken
places a fundamental limit on the accuracy of the period measurement.
Second, there are roughly evenly spaced side lobes.
These side lobes contain spectral leakage due to high frequency
components in the Fourier transform of the original signal.
Third, the total power in the peak of the window function is greater
than the power of the true signal by a factor of a few.
Finally, there are large peaks on either side of the main lobe displace by one
rotation per day. This is due to the one day periodicity in the
observations. The windowing can
cause a problem with period determination since periods very close to
one day and very long periods and appear similar to the null signal
case. Careful study of Figure 2 reveals difference
between the window function and periodograms of these signals. Even
with only 30 samples, periods deviating from a day by 1% are detectable.
For convincing results though, the periodogram requires
the aid of other data analysis. This usually consists of visual
inspection of the raw data and the phased data. To gain a better
understanding of how the observational data behave, simulations were
run using synthetic data.



Next: Simulations
Up: Period Determination
Previous: False Alarms and
Scott J. Wolk
Thu Dec 5 11:30:29 EST 1996
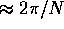 where N
equals the number of samples. The number of samples taken
places a fundamental limit on the accuracy of the period measurement.
Second, there are roughly evenly spaced side lobes.
These side lobes contain spectral leakage due to high frequency
components in the Fourier transform of the original signal.
Third, the total power in the peak of the window function is greater
than the power of the true signal by a factor of a few.
Finally, there are large peaks on either side of the main lobe displace by one
rotation per day. This is due to the one day periodicity in the
observations. The windowing can
cause a problem with period determination since periods very close to
one day and very long periods and appear similar to the null signal
case. Careful study of Figure 2 reveals difference
between the window function and periodograms of these signals. Even
with only 30 samples, periods deviating from a day by 1% are detectable.
For convincing results though, the periodogram requires
the aid of other data analysis. This usually consists of visual
inspection of the raw data and the phased data. To gain a better
understanding of how the observational data behave, simulations were
run using synthetic data.
where N
equals the number of samples. The number of samples taken
places a fundamental limit on the accuracy of the period measurement.
Second, there are roughly evenly spaced side lobes.
These side lobes contain spectral leakage due to high frequency
components in the Fourier transform of the original signal.
Third, the total power in the peak of the window function is greater
than the power of the true signal by a factor of a few.
Finally, there are large peaks on either side of the main lobe displace by one
rotation per day. This is due to the one day periodicity in the
observations. The windowing can
cause a problem with period determination since periods very close to
one day and very long periods and appear similar to the null signal
case. Careful study of Figure 2 reveals difference
between the window function and periodograms of these signals. Even
with only 30 samples, periods deviating from a day by 1% are detectable.
For convincing results though, the periodogram requires
the aid of other data analysis. This usually consists of visual
inspection of the raw data and the phased data. To gain a better
understanding of how the observational data behave, simulations were
run using synthetic data.

