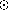 star requires
almost 10 times the variability level as a 1.0 M
star requires
almost 10 times the variability level as a 1.0 M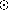 star. Thus, one
is more likely to find periods for either more massive or more active stars.
star. Thus, one
is more likely to find periods for either more massive or more active stars.
The only criterion used for inclusion of a star in the monitoring program was that the star had to be an X--ray source. As such, there may be a bias against observing stars with disks, since the disk might tend to obscure X--rays.
This criterion is a very significant bias if there is a relationship between rotation and activity as has been suggested by several authors. Bouvier (1990) found a power law relation between the X--ray luminosity and the rotational velocity. He also found a similar relation between rotation period and X--ray flux. These relations hold for both cTTs and weak--lined T Tauri stars (wTTs). Bouvier used this to argue that the source of the X--rays is the same in both types of stars. However, the relationship between X--ray flux and rotational period is not clearly established. Walter (1996) points out that this perceived relation between X--ray luminosity and rotation may not be the result of physical connection, but instead it may be the result of an X--ray flux dependence on surface area which is a function of mass. In this case, the smaller (in radius) a star is, the less it radiates in X--rays. Since radius is a monotonic function of mass on the Hayashi track, as mass drops, so does X--ray luminosity. If period is a function of mass, a perceived relation between X--rays and rotation may not tell us anything about the dynamo mechanism.
In addition to the selection effects, several observational biases affect
the final results. First of all, in any given field there were
several target stars. The exposure times were designed to properly
expose the brightest target in the field, usually 11th magnitude at V,
so that 0.5%
photometry would be possible. Generally, noise induced by
fairly poor seeing and humidity conditions, lowered accuracy on the
brightest sources to 1%.
This means that the accuracy of the measurement of a 15th magnitude
star in the same field is less than 10%.
The detection of a period on a 0.5 M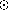 star requires
almost 10 times the variability level as a 1.0 M
star requires
almost 10 times the variability level as a 1.0 M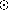 star. Thus, one
is more likely to find periods for either more massive or more active stars.
star. Thus, one
is more likely to find periods for either more massive or more active stars.
Another observational bias is set by the duration of the observing runs. With the exception of the two stars monitored from Mount Stony Brook, all stars were monitored over an 11 night time interval. Because of this, the data are not very sensitive to periods longer than 11 days. The two that are found (R053844-0240 and R053849-0238), are extrapolations based on available data. Simulations with three observations per night demonstrated that a star with a period less than six days could be detected at a signal to noise level of about 2.5. Stars with periods of between six and 12 days required a S/N of about four. Stars with periods longer than 12 days required a S/N > 5 to detect the period. Thus, as the period of the star gets longer, one can only measure periods of heavily spotted stars.
To compensate for these short runs, several observations (3--4) were made of each star each night. Therefore, these data are sensitive to periods of less than one day. I include periods from 2 days down to 0.5 days (the length of the night) in my search window. Such periods were explicitly excluded from period search routines of Bouvier et al. (1993, 1995). This could account for the difference in the period of TAP 26.
Period searches below two days were also generally excluded from the data presented in Eaton et al. (1995), Attridge & Herbst (1994) and Choi & Herbst (1996). This is one of the reasons that the KS test gave a very low probability of the data presented here and those from Choi & Herbst being drawn from the same parent distribution. Additionally, due to diurnal aliasing properties of the data, it is very hard to distinguish between periods near a day and an alias of that period. Figure 1 shows an example of this for R053844-0240. The data folded on the 1.09 and 0.91 day peaks in the periodogram show almost as strong a sinusoidal behavior as those folded on the 12.2 day peak.
The 12.2 day period was chosen as the correct one since it has a smaller deviation from the fit than the shorter ones. Taking these biases as a whole, some of the higher FAP periods listed as just below one day may be just above one day. Also, some 2--4 day periods published by other authors may in fact be < 2 days.
The two data sets presented here have identical selection effects.
The data from the SFRs in the 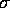 Orionis region and those in Orion OB1a
seem similar in spite of the large age difference.
Orionis region and those in Orion OB1a
seem similar in spite of the large age difference.