BlackBody1D

class astropy.modeling.blackbody.BlackBody1D(temperature=<Quantity 5000. K>, bolometric_flux=<Quantity 1. erg / (cm2 s)>, **kwargs)

Bases: astropy.modeling.Fittable1DModel

One dimensional blackbody model.

Parameters:

temperature : Quantity

Blackbody temperature.

bolometric_flux : Quantity

The bolometric flux of the blackbody (i.e., the integral over the spectral axis).

Notes

Model formula:

\[f(x) = \pi B_{\nu} f_{\text{bolometric}} / (\sigma T^{4})\]

Examples

>>> from astropy.modeling import models
>>> from astropy import units as u
>>> bb = models.BlackBody1D()
>>> bb(6000 * u.AA)  
<Quantity 1.3585381201978953e-15 erg / (cm2 Hz s)>

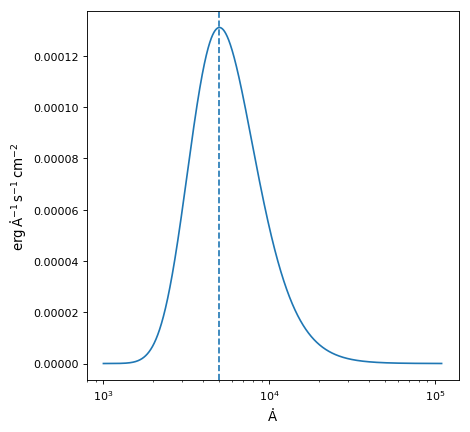
import numpy as np
import matplotlib.pyplot as plt

from astropy.modeling.models import BlackBody1D
from astropy.modeling.blackbody import FLAM
from astropy import units as u
from astropy.visualization import quantity_support

bb = BlackBody1D(temperature=5778*u.K)
wav = np.arange(1000, 110000) * u.AA
flux = bb(wav).to(FLAM, u.spectral_density(wav))

with quantity_support():
    plt.figure()
    plt.semilogx(wav, flux)
    plt.axvline(bb.lambda_max.to(u.AA).value, ls='--')
    plt.show()

(png, svg, pdf)

Attributes Summary

bolometric_flux
input_units	This property is used to indicate what units or sets of units the evaluate method expects, and returns a dictionary mapping inputs to units (or None if any units are accepted).
input_units_equivalencies
lambda_max	Peak wavelength when the curve is expressed as power density.
param_names
temperature

Methods Summary

evaluate(x, temperature, bolometric_flux)

Evaluate the model.

Attributes Documentation

bolometric_flux = Parameter('bolometric_flux', value=1.0, unit=erg / (cm2 s), bounds=(0, None))

input_units

This property is used to indicate what units or sets of units the evaluate method expects, and returns a dictionary mapping inputs to units (or None if any units are accepted).

Model sub-classes can also use function annotations in evaluate to indicate valid input units, in which case this property should not be overridden since it will return the input units based on the annotations.

input_units_equivalencies = {'x': [(Unit("m"), Unit("Hz"), <function spectral.<locals>.<lambda> at 0x116fd9268>), (Unit("m"), Unit("J"), <function spectral.<locals>.<lambda> at 0x116fd9378>), (Unit("Hz"), Unit("J"), <function spectral.<locals>.<lambda> at 0x116fd9400>, <function spectral.<locals>.<lambda> at 0x116fd9488>), (Unit("m"), Unit("1 / m"), <function spectral.<locals>.<lambda> at 0x116fd9510>), (Unit("Hz"), Unit("1 / m"), <function spectral.<locals>.<lambda> at 0x116fd9598>, <function spectral.<locals>.<lambda> at 0x116fd9620>), (Unit("J"), Unit("1 / m"), <function spectral.<locals>.<lambda> at 0x116fd96a8>, <function spectral.<locals>.<lambda> at 0x116fd9730>), (Unit("1 / m"), Unit("rad / m"), <function spectral.<locals>.<lambda> at 0x116fd97b8>, <function spectral.<locals>.<lambda> at 0x116fd9840>), (Unit("m"), Unit("rad / m"), <function spectral.<locals>.<lambda> at 0x116fd98c8>), (Unit("Hz"), Unit("rad / m"), <function spectral.<locals>.<lambda> at 0x116fd9950>, <function spectral.<locals>.<lambda> at 0x116fd99d8>), (Unit("J"), Unit("rad / m"), <function spectral.<locals>.<lambda> at 0x116fd9a60>, <function spectral.<locals>.<lambda> at 0x116fd9ae8>)]}

lambda_max

Peak wavelength when the curve is expressed as power density.

param_names = ('temperature', 'bolometric_flux')

temperature = Parameter('temperature', value=5000.0, unit=K, bounds=(0, None))

Methods Documentation

evaluate(x, temperature, bolometric_flux)

Evaluate the model.

Parameters:

x : float, ndarray, or Quantity

Frequency at which to compute the blackbody. If no units are given, this defaults to Hz.

temperature : float, ndarray, or Quantity

Temperature of the blackbody. If no units are given, this defaults to Kelvin.

bolometric_flux : float, ndarray, or Quantity

Desired integral for the blackbody.

Returns:

y : number or ndarray

Blackbody spectrum. The units are determined from the units of bolometric_flux.