The first step is to determine the best channels to use for the hardness ratio. In his initial report on the HRI spectral response Fraser concludes that the ratio (counts in channel 1-5)/(counts in channel 6-11) is the most senstive energy indicator. This is true for most sources. However, the optimal channel selections should be checked for each observation. The optimal ratio is one in which the two bands (hard and soft) are seperated as cleanly as possible. An example is given in Figure 4. Here we show three plots. The top left panel shows the probability that a photon will be detected in channels 1-5 as a function of energy (solid line) and the probablity that a photon will be detected in channels 6-15 (dashed line) for the 61 Cyg sequence rh201950n00. The other two panels show the same plot, except that probability is shown for channels 1-6/7-15 and channels 1-4/5-16. These values were derived from the response matrix new_resp.fits. This plot shows that the most senstive indicator is channels 1-4/5-15, which corresponds to a ratio of counts above and below 0.6 keV. A recipe for creating channel boundary plots is given in Appendix A
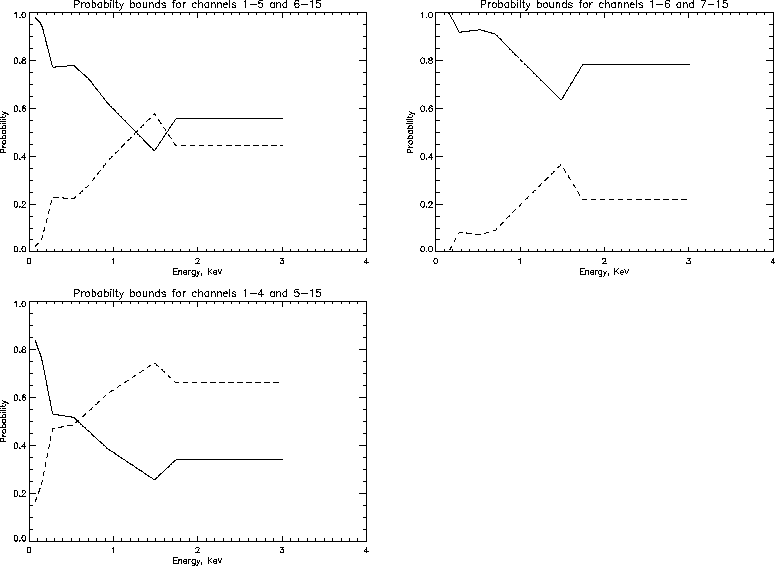
Figure 4: The top panel shows the probability that a photon will be detected
in channels 1-5 as a function of energy (solid line) and the
probablity that a photon will be detected in channels 6-15 (dashed
line) for the 61 Cyg sequence rh201950n00. The other two panels show
the same plot, except that probability is shown for channels 1-6/7-15
and channels 1-4/5-16.
The next step is to produce simulated data files. This can be done within XSPEC using the ``fakit'' command. Required inputs are parameters of the spectral model and the response matrices. To ensure that the counting statistics are the same for the simulated data files as for the real data, input a model normalization/exposure time combination that produces an overall countrate in the simulated files approximately equal to that in the real data file. It is then possible to compare the distribution of simulated hardness ratios with that of the real data.
Figure 5 shows the results of 4 simulations for 61 Cyg. The models used in the simulations were Raymond-Smith plasmas with temperatures of 1.0, 0.3, 0.4, and 0.5keV. One hundred fake data files were produced for each model. The ratio of counts in channels (1-4)/(5-15) for the real data was 0.86. The hardness ratios of an 0.4 keV plasma group around 0.85, as might be expected from the fit to the HRI spectra and the PSPC results. However, the hardness ratio is also consistent with an 0.5 and 1keV plasma. Without prior knowledge of the source, we would conclude that the spectrum was consistent with a temperature of 0.4keV, but could not rule out a temperature as high as 1keV.
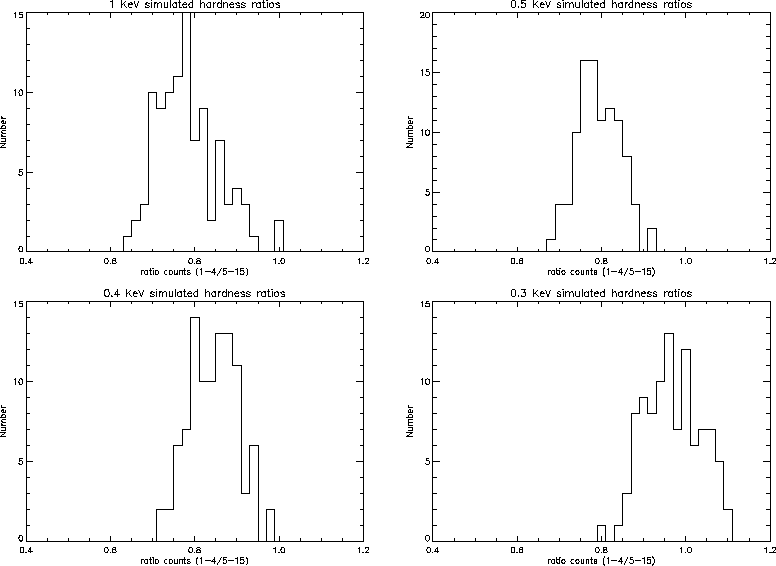
Figure 5: Histograms of hardness ratios produced from simulated data
files. From top left to bottom right the models are; 1 keV, 0.5keV, 0.4keV, and
0.3keV RS plasma. The real spectrum has a ratio of 0.86.