Latitude is easy to understand with a globe in front of you. Notice you can divide the globe in half anywhere so that it will make two symmetrical pieces. We call the imagined horizontal line running around Earth's middle the equator. See that any other horizontal lines imagined above or below the equator divide the globe unevenly. Such non-equatorial lines are referred to in terms of their distance from the equator. A line called 20° North would tell you that this line is somewhere north of (or "up" from) the equator at a distance measured not in miles, but in degrees. In other words, this distance represents some angle. Where is this angle measured from? If we pick a point on the equator and connect it back to the center point of the globe, we would have a kind of line commonly called a radius. This radius would have an angle of zero degrees, because it is stretched flat from the middle of the Earth to the equator. A line (or radius) stretching straight up from the Earth's center to the North pole of the Earth would measure 90° N. Can there be any angle from the Earth's center higher than that? No. What if we connected all the points 20° above the equator to the center of the Earth? They too would make a radii, but would be at 20° angles to the flat radii running out from the Earth's center to the equator. This is what is meant by 20° N latitude.

The height of the Sun above the horizon is determined by several things, one of them being the position of the viewer on the Earth. The further the viewer is from the equator, the lower the Sun will appear in the sky. To understand this, we must first recall that the Sun is a huge sphere 93,000,000 miles away. Its light comes to us as direct rays. With a non-tilting Earth, this would mean the direct rays would hit the equator dead on, and the viewers there would see the Sun directly overhead, while elsewhere along the curved Earth other viewers would see the Sun at some height over the horizon, but not directly above them like at the equator. This is easier to understand if we think about an imaginary line cutting the sky in half. This sky equator would be right over the Earth equator, slicing the sky into two half-spheres, as if the Earth equator were a big disk stretching out into space. The Sun would travel along this sky equator around and around right above the Earth equator if the Earth were not tilted. Those of us not living on the Earth equator would have to look somewhere other than directly overhead in the sky to see the Sun's path. Just as we would have to look lower on the Earth (in the northern hemisphere) from where we are to find the Earth's equator, we would have to look lower in the sky (as opposed to directly overhead) to find the Sun. With globe in hand, imagine that sky equator disk jutting out from the Earth equator. Now, imagine you are walking from the equator north, to someplace like Boston. When you began, you were directly under the Sun. In Boston, your sky would be different, with the Sun's path in the South part of the sky, closer to the horizon, and not overhead.

The other factor determining the height of the Sun's path is the Earth's tilt. Most of the planets in the Solar System spin on an axis which is tilted over compared to the plane in which they orbit around the Sun. The tilt of the Earth's axis is 23.5°. This is a rigid tilt, which means that the Earth always seems to tilt over 23.5° in one direction only. (Refer to the diagram for a visual). So, as it goes around the Sun, this tilt makes the Sun height change an awful lot during the year, since tilting towards or away from the Sun causes the Sun to appear respectively higher or lower in the sky. But understand that the Earth is not rocking back and forth! It is just the fact that the forward tilt axis (of the North pole) is always along one straight line, while the Earth is going around the Sun in a roughly circular path. This means the Sun will sometimes be in line with the forward tilt of the pole and other times it will be not in line and still other times it will be opposite of the forward tilt direction.

When the Earth is in a section of its orbit around the Sun where the Sun is in line with the forward tilt of the pole, then places in the Northern Hemisphere have a higher Sun in the sky, hence a longer arc for the Sun to go through across the sky. This results in a longer amount of sunlight (longer daylight time in summer), and hence a longer time for the Sun to heat up the surface. This causes warmer temperatures; this is summer. In contrast, when the Earth has orbited around the Sun to the section where the Sun is in the opposite direction of the forward tilt of the pole, places in the Northern Hemisphere will see a lower path for the Sun in the sky, hence a shorter arc for the Sun to go through across the sky, hence a shorter time to heat up the surface. This causes cooler temperatures, this is winter. So, what is happening to the Southern Hemisphere? With the Sun's view of the Earth's top tilting back, the southern areas of the planet are tiltling towards the Sun, just like bending backwards and having your tummy sticking out! So, the Southern Hemisphere is getting warmer with a higher Sun arcing a longer distance across the sky. What about when the Sun is in line with the tilt arcing towards it? Well, then the Southern Hemisphere is having winter.

What about in between these two seasons? The Earth has moved into a section of its orbit where the Sun is not in the direction of the forward tilt of the pole, nor is it in the opposite direction. There is no extreme Sun height during these times of year which we call fall and spring. For one day in both the spring and the fall, the Sun strikes directly over the equator. No part of the Earth is tilting to the Sun. The only affect on the height of the Sun is the fact that the Earth is a sphere, and we all live somewhere along the curve. The special day is called an equinox, meaning equal night and day times. The day is exactly 12 hours long, making the night 12 hours as well.

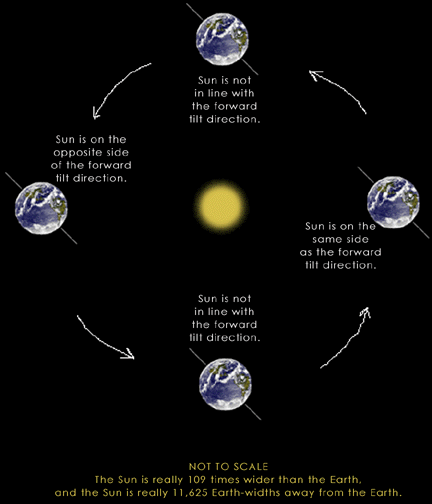This is a diagram of the Earth-Sun-Tilt relationship. Imagine that you are looking at this three-dimensional system at a 45° angle above it and over a year's time. Because it is a diagram, it is not a perfect representation. But we hope it will be helpful in illustrating the text. Notice that the Earth's tilt is always directed towards one place (in this model, it is towards the left. But if we changed our perspective by looking underneath or to the side, saying the tilt was "towards the left" becomes meaningless. This is a clue for you that models are not perfect, and we have to be careful in how we talk about them.) The Earth orbits around the Sun during the year, and so the Sun is not always in the direction of the North pole's tilt. This is what causes the seasons, and in this drawing on the right, when the Sun is in the direction of the North pole, the Northern Hemipshere has summer.

Download

---

---

Gather everyone around so that they can see the shadows cast by the little trees. Are the shadows the same or different? Turn the globe so that all of the places with trees get the light. Which shadows are the longest shadows? Which shadows are the shortest? Where do the shortest ones all seem to be? Around the middle of the globe. And the longest are all around the poles. Why? Move to the blackboard or a map with some blue-tak. Where do you think we could put trees on this world here so that they'd have different shadows? Let them stick trees on this flat object. Aim this towards the light as well, but at a slight angle (or no shadows, right?). Are any of these shadows on the paper different from each other? They will be the same length. Have them look at both the paper and the globe. What is the difference between these two worlds? One is flat the other is round, they will say. Which one is like our world? It is not important that they know the real answer, only that they keep thinking about it for a while as the year continues.

Where people are located on the Earth determines how much Sun they get in a day. Who do you think gets less Sun? They may want to think some about the coldness or hotness of a place. Which place is hotter, Florida or Alaska? Where are they on this globe? Who has longer shadows? Who has shorter shadows? How did we make long or short shadows when we were playing with the flashlights? They may recall that when they tipped the flashlight up or down, they could change the shadow lengths. Relate this to people living tipped up or down from the middle of the world.

---

---

The class should be divided into three or four groups. In each group, they should choose a place somewhere in the world other than their home town, maybe where they have family or friends. One group should locate their place on the hanging globe and help you place a small golf tee (head down) to the spot with blue-tak. You should place a tee at the school's location as well. What are the golf tees supposed to represent? Small versions of the sun stick!

How would we make the sun stick shadows on the globe? Students will say move the overhead projector or the globe. Which is easier? Answering this question may help us understand why the Sun's apparent movement is caused by the Earth spinning and why the Sun is not orbiting around the Earth instead--the Sun is large and much harder to move! Slowly turn the globe counter clockwise so that each tee "sees" the Sun rise in the east and set in the west. Is the pattern of shadow lines from the tees similar to the pattern cast by the sticks in the previous Threads? What are the differences between the golf tee shadows at the school's location on the globe and at the location picked by the first team? Why is this happening? Does the shape of our world make this happen?

Attach a tee to the second team's spot on the globe. Slowly turn the globe again. Does the light reach this tee before or after it reaches the first team's tee or even the school's tee? So, does the Sun rise earlier or later in this new location? Are both team's tees always in light together or are both always in darkness together? Or can one be in light while the other is in darkness? What if the two tees were on opposite sides of the Earth?

Continue placing the other team's tees on the globe and asking the same questions. When they are all attached and examined, ask the students what they think is making the shadows shorter or longer? Which teams had the longest shadows? Where was this team's tee? What makes its location different than the other tees? Students should begin to articulate the differences, some unrelated and others crucial.

Ask students to remember how they were able to make longer or shorter shadows when they used flashlights. Tilt, yes--now your students may begin thinking about the tilt of the tees. However, it may not be very obvious that the curve of the globe is the same as the tilt of the tee. This is OK.

Ask them how they would move either the overhead projector or the globe to get shorter shadows. They will say lift the projector. Could you really lift that thing! Then what is another solution? You could tilt the globe. Select the school's tee so as not to appear to be favoring any single team, and tilt the globe. Ask the students to be watching the shadow lengths carefully. What happened when the globe tilted back? How short was the shadow?

Attach two more golf tees to the globe at various latitudes but along the school's meridian of longitude (so that you can keep your tee there for consistency). One should be on the equator and one should be near the North pole. It is not necessary at this juncture to call these positions by their map names. Face them into the overhead projector. What do the shadows look like for the different tees? Whose shadow is longest, the top, the school's, or the bottom? Why is this?

Viewing the globe from the side, can we see how the tees appear to be along a curve? Get a textbook and blue-tak three more golf tees to the front of it. Hold it next to the globe so that the tees are pointed straight at the light. What are the shadows like? There are none! What could we do to make some? Tilt the book? Tilt the book and have students look at the shadows. There are shadows now, but all three are the same length.

How do we know if we're spinning the globe in the right direction? Can they see the sun-stick shadows moving in the familiar direction? What is the shadow like at the equator? What about at your latitude? Ask the students what life is like at the different latitudes used. What are the trees like? The weather? The animals? What if the North Pole were pointed towards the Sun? Where would it be day and night? Would all locations still have both day and night?

---

---

Have every student choose a state capital or country somewhere in the world. If you are using the packet only, use capital cities of the United States, and encourage the choice of Hawaii, Alaska, and the Virgin Islands. Where is your city on a globe? Provide globes on every table or a big globe in the front of the class. Put little tabs on your city or at least mark it on a photocopy of a world map. Before you look up your city in the packet (or on the Internet), do you have any predictions about how long you think the daylight will last at your chosen location when compared to the length of daylight at the school for today? What is your reason? In their journals, have them write down their city and what country it is in. Suggest that they write down what they think about the length of day.

Give students the appropriate entry in the packet and explain to them how the packet is laid out. If you are using the Internet, let them take turns at the computer gathering data from the Internet site for their capital city. They should write their numbers down carefully somewhere or even print out the page from the computer screen. Keeping a table of the numbers would be best done by older students. Can each of us calculate the length of daylight for our chosen cities? When each student has a length of daylight for his or her city, begin your own table of daylight times, but with a row for each city and a column next to this for the length of daylight. And later, when it is realized that thlatitude is linked to the length of the day, add one more column for the latitude.

Going around the room, have each student call out his city and the length of day he calculated for it. Write this in the table. After a few cities are discussed, the students will definitely notice there is a difference in the lengths of day. Locate on the globe the first few cities that have been mentioned. Does anyone see why these places might have different amounts of sunlight during the day? They will list those things which are different about where each city is. But the question is, of course, why should those differences have any influence over the sunlight? Gather more cities and find them on the globe. Which cities have the shortest amount of daylight? Where are they? Which have the most amount of sunlight during the day? Where are these cities? If you have cities in both the northern and southern hemispheres, there will be a definite pattern of average daylight times for cities nearer the middle of the globe and longer days for cities on one half of the globe only. The cities on the other half will have shorter days. What is happening?

Place small blobs of blue-tak with toothpicks of equal length on a few of the labeled cities which have the greatest differences in daylight times. Shine a very bright overhead projector or lamp onto the globe and hit those cities. Can everyone see the shadow lengths of the toothpicks at these different cities? Is there a pattern? Is there any connection between the daylight time and the sun stick lengths? What might be the situation here? It may be necessary to step back and think about what it looks like to do the sun stick measurement.

What does the shape of the world look like outside? Does it look like a sphere out there? No, it looks rather flat! Let's try to create flat areas for our cities here. Get a small square of stiff paper like manila or oaktag paper. Put the paper under one of the cities so that it lies flat on the point where the city blue-tak is and creates a tangent plane at that point. (A tangent plane is a plane touching only one point along the surface area defined by a sphere.) Then make another for the other cities. Are these flat views the same as each other? No, but they are what each person sees at that spot, flatness. What is the difference between the flat areas? How do you have to move your head to be flat with them? There is a tilt of some kind here. Does that change where the Sun appears in the sky? If it is not painful for the eye, have students come up and move their heads so that they are flat with the city and then look at the light source chosen to be the Sun. How high does it look compared to the background of the classroom? The higher you tilt on the globe, the lower the Sun appears. Do you think that people who see the Sun very low have more or less sunlight during the day? Less. Where are those places on the globe? What were the daylight times for those cities?

There will still be confusion regarding the strangeness of how the two halves of the Earth have the greatest difference in daylight time. Ask them directly what would happen to the shadows if you tilted the globe even more in one direction? In some places, the Sun will seem higher, and in other places, lower. Discuss this until the students can understand the changing perspective.

Is there a good way of dividing the globe into pieces that we could talk about more easily than saying, "Well, at the location of Tokyo ..." How do we give locations of cities anyway? Students will call out the latitude and longitude idea. Can they point out on which latitude lines the various cities on the map lie? Why is the equator zero? What does zero mean? Why isn't zero at the top or bottom? And why are the latitudes in degrees?

Thinking about this convention might be difficult. When we did the sun stick triangles, we used the flat line of the shadow on the ground as the bottom of the triangle and said the Sun's height, measured in degrees, was the size of the angle -- also measured in degrees -- made when a line drawn from the position of the Sun meets the shadow line on the ground. But where on Earth would you start from, where would "zero" be? Where on the Earth would the Sun, at mid-day, be most likely to cast "zero" shadow? In other words, where are you most likely to find the Sun directly overhead? At the equator, the line drawn around the middle of the Earth which divides the Earth into two equal parts. If you take a line drawn from the equator to the center of the Earth as having an angle of 0 degrees, then you can measure the latitude of any place on Earth above or below the equator by measuring the angle between a line drawn from that spot to the center of the Earth and a line drawn to the center from the equator.

Hold a globe to the blackboard and have someone help you trace the outline of the globe on the board. Draw a careful line in the middle of the circle on the board. What is this? The equator, of course. Mark the center of the circle on the board. Using protractors fixed on the center point, can the students mark lines along the circle where 20° and 40° etc. all hit? When these marks are made, extend them out longer to the globe circle, so that they will be clearly visible. Draw horizontal lines across the globe which hit these marks on the edges of the circle. Then hold the globe back on the board over the trace and see if the marks match those corresponding latitude lines on the globe. Bingo! That is how all this is works.

Can a latitude line give us the exact location of a city on the globe? If you say the city is at 42° north latitude, how many cities are also on this latitude? What else do we need? What about those longitude lines? Look down on the top of the globe. There are rays coming out of the North pole as well. The same exercise could work here, however, the longitude conventions use an 180° basis instead of the 90° basis used by the latitude system. But the idea is the same: rays made from angles drawn around a circle. So, how could you classify two cities such as Beijing, China and Denver, Colorado? Then try Oslo, Norway and Pittsburgh, PA?

Using the equinox data collected by you or your class, follow the procedures for finding the height of the Sun in degrees outlined in This is a Stickup! OK, so we've got some angles measuring the Sun's height. What can we do to think more about how this relates to the whole world?

Ask the students about their Stickup set-up. What did it look like? Draw on the board the stick and a shadow coming off to the right. Where is the sunlight coming from? They should be able to tell you that there is sunlight coming over the stick. Draw rays coming over the stick and hitting the stick or going over it to make the shadow. Draw this carefully so that the rays hit the stick and we can tell where the shadow will be by making that last set of rays skim over the top of the stick and mark the end of the shadow.

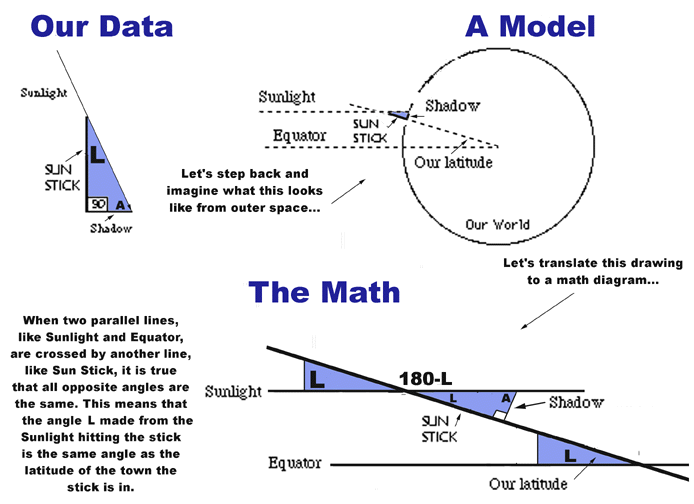
Are the lines straight? Is this what was happening at our set-ups? Does this look confusing? Do we need all of these sun rays? Which ones are the most important to think about here? Erase all of the rays except the one that points directly from the top of the stick to the Sun. What is the shape being made by the lines of sun stick, shadow, and sunlight line? Students should be able to tell you this from their experiences with the previous Thread that it is a triangle. But can they tell you what this would look like from outer space? Please refer to the diagram at the end of this Thread for help recreating it on your board.

Where is the angle that marks the height of the Sun? They will point to the end of the shadow and how it can be linked to the top of the stick and then back to the Sun. Good.

On the board, draw a large circle representing the Earth with a line through the middle and extend the line out from the circle quite a bit. What special mark on the Earth is this? That is the equator. Draw a short line sticking straight out of the side of the circle (about at your latitude, basically), somewhere above the equator line. Imagine this is the stick we stuck in a can. Connect the stick line to the center of the world with a dotted line so that we can think about where the stick is with relation to where the equator is. What does that angle made by the Equator and the stick line mean about where the stick is on the Earth? It means it is the same number of degrees above the middle, or equator, which is the same as saying it is at that latitude. Do we see that? Take another look at the drawing at the end of this section, if this is not clear. Let's mark a dark L in the angle; L for latitude. Cool.

Where is the Sun? Many will point off to the side somewhere. Draw a circle there. Is the Sun this small? Is it this close to the world? Maybe we should make it bigger and move it further away. Use the whole side edge of the blackboard as the Sun's edge and draw lines of sunlight coming from this edge to the world. The lines should be straight and parallel to the Equator line. This allows us to see that the rays are very straight when they hit the world and the stick.

What can we notice now about this ray and the line of the Equator? They are parallel, or flat with each other. What about the stick? It's extension crosses both the lines. Let's try to zoom in here.

Below the big world drawing, simplify the diagram by drawing two parallel lines crossed by another line like the stick line. Label them like they are labeled in the world drawing, including marking where L is. Does everyone agree that the lines you've just drawn are really a simpler version of the drawing above them? This is a math drawing, and it will help us to talk more easily about triangles.

Do any of these other angles look like L? It is difficult to see. How could we check it out? Make a right triangle out of heavy paper so that it fits perfectly into this L angle and is big enough to be seen across the room. In other words, make a triangle with one angle 90° and another angle L°. Mark L at the L angle and on the other side of the triangle as well. Where does this fit into our drawing? Where else might we be able to fit this triangle in the picture? Have students come up to the board and try to fit the triangle into some place of their choosing. They will find that it fits into the space made by the stick's end and the ray of sunlight. Flip the triangle over. Is this angle L the same as it was before? Yes. It can't be different because the triangle did not change. This is like flipping shapes from Guess My Shape. The shape can look different even if it does not change but is only flipped or rotated. In the drawing provided, the shaded area shows that this is indeed the same triangle.

They will then find that the triangle shape fits into all angles directly across from the L one. Great. This means something important. This means that the angle of the latitude is the same as the angle made by the Sun line and the top end of the sun-stick. But in This is a Stickup, we only measured the angle of the shadow line and the ground, and not the angle of the stick and the ray of sunlight, which we now know as L. How could we ever find L?

What is the angle made by the sun stick and the ground for every sun-stick measurement? Was the stick straight up? Straight up means what angle? Can everyone find straight up with a protractor? What is the angle? 90°. OK. So, now we know two of the angles in the triangle: we know the one we measured at the shadow and the ray of sunlight and we know about the 90° made by the stick and the ground. What is the other angle, L? Does anyone suggest just looking up our latitude in the atlas? Why not? Does anyone think we can really discover it ourselves? Nah, that's what scientists do or something, right?

Hand out paper right triangles of different side lengths. Have teams measure each angle in each triangle. Add the three angle values together. What is the total of each team's triangle? 180° always. So here's a clue. If we know two out of three angles of a triangle, we can find the third angle. How? Let them puzzle this for a while, and then if they can't come up with the solution, ask them to add up the angles they do know. How much of the total do they have? Is that 180°? How much more until they can get 180°, or in other words, what is 180° minus their sum? Tah-dah!

Back to the sunstick problem. What was the angle of the stick with the ground? 90°. Write this into the sunstick triangle drawing. What is the angle of the Sun's height at midday on the equinox, (that is, the angle of the shadow tip and the ray of sunlight)? We will have to look at our data from Stickup to get this value; we have three different ways of finding it, remember? Write this angle in the drawing as well. Add them together. What is the third angle, or what is 180° minus our sum? Write it in the sun-stick triangle and then move it over to the corresponding place on the simpler parallel line drawing. Which angle is like this missing angle? That is angle L! It must be our latitude. How do we know if we are right? Who looked it up earlier? How did we do? We rule.

Now for some predictions. What would happen to the shadow lengths if the Sun moved up or down? Or if the Earth somehow tilted over and back? Do you think these things happen? If we take length of daylight and shadow length measurements every week for the school year, do you predict we will we see anything change?