
Guess My
Shape
 Understanding how light hits things of different shape and form necessitates an understanding of shape and form. Becoming familiar with the shapes around us and having a language to talk about them helps us when we describe other things which are happening in our world. The National Science Education Standards suggest introducing the rectangular solids in elementary school and the manipulation of shapes and perspectives throughout the school year. Older students will benefit from the application of math skills to shape and structure. Vocabulary words which can be introduced to help us talk about our experiences are shapes, edges, sides, cylinder, sphere, triangular solid, rectangular solid, cone, pyramid, and cube.
Understanding how light hits things of different shape and form necessitates an understanding of shape and form. Becoming familiar with the shapes around us and having a language to talk about them helps us when we describe other things which are happening in our world. The National Science Education Standards suggest introducing the rectangular solids in elementary school and the manipulation of shapes and perspectives throughout the school year. Older students will benefit from the application of math skills to shape and structure. Vocabulary words which can be introduced to help us talk about our experiences are shapes, edges, sides, cylinder, sphere, triangular solid, rectangular solid, cone, pyramid, and cube.
 There are several basic shapes in our world which show up time and again. We call these the regular solids because their construction is from simple shapes like circles, triangles, and rectangles. To make one of these shapes is to imagine a triangle, say, sitting flat on the table as if cut out from a piece of paper. Flat as it is, it is nearly two-dimensional. What if you could give it height? Imagine being able to grab hold of the three sides and stretch them upwards. From
There are several basic shapes in our world which show up time and again. We call these the regular solids because their construction is from simple shapes like circles, triangles, and rectangles. To make one of these shapes is to imagine a triangle, say, sitting flat on the table as if cut out from a piece of paper. Flat as it is, it is nearly two-dimensional. What if you could give it height? Imagine being able to grab hold of the three sides and stretch them upwards. From  above, it would still look like a triangle, but from the sides, it would look like a building with three sides. This is called a triangular solid. The same technique is used to make a cube or cylinder. These shapes are often called "prisms", but are quite unlike rainbow prisms, so we should not refer to these shapes as such. Instead, they are rectangular solids, because a shadow cast from the long side is always a rectangle.
above, it would still look like a triangle, but from the sides, it would look like a building with three sides. This is called a triangular solid. The same technique is used to make a cube or cylinder. These shapes are often called "prisms", but are quite unlike rainbow prisms, so we should not refer to these shapes as such. Instead, they are rectangular solids, because a shadow cast from the long side is always a rectangle.
To make something like a pyramid or cone, you must imagine a similar procedure. Instead of stretching the sides up to make the solid, you imagine that you pull them up and together to a point at the top. Or imagine you cut paper into smaller and smaller versions of the flat shape and place them on top of one another until you have cut out a single point, which is the very top. So, a four sided pyramid is a square onto which is placed a smaller square and so on. The sides slope as the size of the square shrinks. The same with a cone, but you start with a circle as the flat shape and build up on that.
Pulling shapes through a third dimension means that light shining on these shapes can fool the eye when looking at their shadows. The shadow cast by a light shining on the face of a triangular solid will produce a rectangle. If you knocked the triangular solid on to one of its long sides and cast a shadow from a light shining at one of its ends, you would see a triangle. This is the nature of the regular solids. They have the capacity to fool you when seen only in shadow.
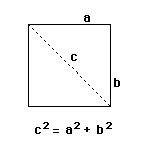 Thinking about the way light hits objects is a good way of thinking about the geometry of these solids. In math, we say that the length of the diagonal cut across the face of a square, let's call it "c", is equal to the square root of the squared lengths of the two sides, a and b. This means that the diagonal is longer than the sides by a little bit. You can find this out yourself with shadows cast on a rectangular solid. If the light is aimed at a side of the solid, the shadow will be a certain width.
Thinking about the way light hits objects is a good way of thinking about the geometry of these solids. In math, we say that the length of the diagonal cut across the face of a square, let's call it "c", is equal to the square root of the squared lengths of the two sides, a and b. This means that the diagonal is longer than the sides by a little bit. You can find this out yourself with shadows cast on a rectangular solid. If the light is aimed at a side of the solid, the shadow will be a certain width.  However, if the solid is turned slightly so that the light is aimed at a corner, the shape of the shadow will still be slightly wider than before. This is the nature of the projection effect of shadows cast from different angles of a rectangular solid.
However, if the solid is turned slightly so that the light is aimed at a corner, the shape of the shadow will still be slightly wider than before. This is the nature of the projection effect of shadows cast from different angles of a rectangular solid.
The ability to roll is something only the circle-based solids have. We cannot talk about corners with these shapes, as there are none. There are edges and surfaces, but no corners. A corner is a point where in flat space, two sides would meet. In three-dimensional space, it is where 3 or more edges meet. An edge is a meeting of two sides, or faces, like the spine of a book or the sharp lines down the cube.
 For Kindergarten through second grade, this Thread focuses on manipulating shapes and sorting objects. This is a great exercise for this age group. They are quite capable of sorting by size and are learning about classification. Geometrical classification by shadow casting may be a bit too complex for them, because children at this age tend to find hierarchical categories confusing. In part because, they tend to assume that categories are mutually exclusive! Superordinate categories create the most difficulty.
For Kindergarten through second grade, this Thread focuses on manipulating shapes and sorting objects. This is a great exercise for this age group. They are quite capable of sorting by size and are learning about classification. Geometrical classification by shadow casting may be a bit too complex for them, because children at this age tend to find hierarchical categories confusing. In part because, they tend to assume that categories are mutually exclusive! Superordinate categories create the most difficulty.
 Let's play with shapes in the light to get a feel for shadows of shapes.What is a cube? Which of these shapes are round in some way? How could you sort these objects into groups? What are some things about these shapes that make them different from other shapes? What names would you give for these shapes?
Let's play with shapes in the light to get a feel for shadows of shapes.What is a cube? Which of these shapes are round in some way? How could you sort these objects into groups? What are some things about these shapes that make them different from other shapes? What names would you give for these shapes?
 A tabletop full of geometric solids and their flat counterparts is a good visual. If there are enough shapes, one set at each group table would be great. How could we sort this group? Students may find links between the triangle and the pyramid or the cone and the pyramid.
Can anyone explain why they made the grouping that they did? What does the group look like when placed on the overhead projector? Is there a way of making a group on the overhead projector whose shadows look alike?
A tabletop full of geometric solids and their flat counterparts is a good visual. If there are enough shapes, one set at each group table would be great. How could we sort this group? Students may find links between the triangle and the pyramid or the cone and the pyramid.
Can anyone explain why they made the grouping that they did? What does the group look like when placed on the overhead projector? Is there a way of making a group on the overhead projector whose shadows look alike?
How do some shapes when put together look like other shapes? What kinds of pictures can we make from just moving these shapes around? Where have we seen these shapes in the world? Why aren't tires made from cubes? Why aren't ice cream cones made from box shapes?
What is the shape of our world?
They will likely say round. What is round? Have them draw the world as seen from a rocket in space.
What colors did you use? What sizes would you see? How many of you put more planets in or made a crescent moon?
Have them talk to you and the class about their drawing. Most every child will have drawn a circle Earth.
Hold up a paper plate and a ball. Which one of these is round? They will say both are, but the world is like the ball.
How do they know that? What would be true, then? Could you walk all around it? Could you sail around it? Could you dig through it? What if the world were like the plate? Could you travel around it, or might you fall off the edge?
Have them make clay or clay substitute planet Earths.
What kinds of things are on the Earth? Water, land, ice, clouds, air? What does light look like when it hits the world shape? Make a mark for where you are on your world. Face your mark towards the light of the projector. What time of the day is it for you? Is there someone on your world having night? Where? Make your mark on your world have night. Are there other people on your world having day while you have night? How much of your world is having night with you? Is this how it works on the big world?

 This age group can think about multiple variables and is capable of imagining other viewpoints and places. For this age level the Thread is focused on speculating about projection of a shape before jumping right into shadow images of them. It engages students in thinking about the function of edges, sides, and corners.
This age group can think about multiple variables and is capable of imagining other viewpoints and places. For this age level the Thread is focused on speculating about projection of a shape before jumping right into shadow images of them. It engages students in thinking about the function of edges, sides, and corners.
 What is a three-sided shape? What is a four sided shape? what is the shape of our world?
What is a three-sided shape? What is a four sided shape? what is the shape of our world?
Gather the sets of rectangular solids into groups and give them out to teams of students at desks. Have them list the different groups of shapes in their pile: which have sharp edges, which can roll around, which have four sides, five sides, etc. They will find many different ways of classifying their shapes. Have them talk to the class about their shapes and the groups they made from them.
 What do shadows of these shapes look like? What if the shapes were not sitting on the paper and were instead floating in space? What would the shape of the shadow of our world look like? It is in space with a big light source shining on it. Shouldn't the Earth have a big shadow behind it?
What do shadows of these shapes look like? What if the shapes were not sitting on the paper and were instead floating in space? What would the shape of the shadow of our world look like? It is in space with a big light source shining on it. Shouldn't the Earth have a big shadow behind it?
Block the overhead projector from the class with a cardboard shield so that they can't see what sits on the projector but can see the projection. Put a shape on the table of the projector and have them try to guess the s hape that is sitting there from the projection. It may be hard to figure it out because of how sometime two very different shapes can make similar shadows. Ask them which shape this could be and why. For example, a triangular solid sitting lengthwise on the projector table will look like a rectangle. Ask them what they could do to be really sure of what the shape was, besides moving the blocking screen you have constructed? They will hopefully say to rotate the object or turn it over on the projector table. A triangle will show up, and then it is obvious. Lift the shape so everyone sees it and go to the next.
hape that is sitting there from the projection. It may be hard to figure it out because of how sometime two very different shapes can make similar shadows. Ask them which shape this could be and why. For example, a triangular solid sitting lengthwise on the projector table will look like a rectangle. Ask them what they could do to be really sure of what the shape was, besides moving the blocking screen you have constructed? They will hopefully say to rotate the object or turn it over on the projector table. A triangle will show up, and then it is obvious. Lift the shape so everyone sees it and go to the next.
Play around with these shapes, asking if this is the shape of the world. Keep the sphere last. When you put the sphere on, ask them which shape this is.
It is the sphere or ball shape. This is the shape of the world, so what does that mean about its shadow as cast behind it through space? Let's be sure. No matter how you rotate the sphere, it always casts a circular shadow. So, if the Earth's shadow were to hit anything, it would be a circle-shape, and that would let us know we were right about the shape of the world. Are there any other shapes that can make a circle shadow?
Put a quarter coin or other larger circle shape on the projector table. You see a circle. How can you be sure? You will have to turn it or rotate it. It is then a thin line.
Does the world ever turn around? What would that mean about its shadow? If it were a flat circle, then its shadow will change from a circle to a line. But if it is a sphere, its shadow should always be a circle. Is there anything in space the Earth's shadow would hit? Is there anything that is somewhere close by us in space? The Moon is the closest object to us in space. Does it ever get in line with the Earth's shadow?
(Please note: that many models of the Solar System show the planets' orbits all in line with the Earth's as well as cramming all of the planets very close together. These models have confused and misinformed students and teachers alike for decades.)
If there is a lunar eclipse soon, this obviously would be a great introduction to it. Otherwise, locate pictures of past eclipses.
What is the shadow's edge shape? It is definitely circular. What does that mean about the shape of our world? Cool.
We have provided supplementary material about moon phases as well, to show they are not caused by the Earth's shadow.

 We will approach this Thread from the geometry of the light/solids interaction. Projection from two dimensions to three or vice versa is possible with this age group, as is trying to relate this to how light "sees" objects in the third dimension. Manipulation of rulers and pencils and working carefully in groups is easier for this age group as well.
We will approach this Thread from the geometry of the light/solids interaction. Projection from two dimensions to three or vice versa is possible with this age group, as is trying to relate this to how light "sees" objects in the third dimension. Manipulation of rulers and pencils and working carefully in groups is easier for this age group as well.
 What are shapes? What makes a shape three-dimensional? Why are shadows the outlines of objects? Why do they seem to sometimes not quite look like the object they are hitting? When light travels past an object, it catches the edges of the object. Is there a way we could make "shadows" just by thinking about the outlines of objects?
What are shapes? What makes a shape three-dimensional? Why are shadows the outlines of objects? Why do they seem to sometimes not quite look like the object they are hitting? When light travels past an object, it catches the edges of the object. Is there a way we could make "shadows" just by thinking about the outlines of objects?
 Draw a square on the board. How can I make this square look like it is three-dimensional? Hopefully they will say you need to give it some kind of depth. Extend its sides outward and then connect them again in a square until you have a cube.
What is this shape called?
Hold up a wooden cube block and orient it to the drawing. Draw a triangle and repeat the depth idea until there is a triangular solid. Hold up a wooden triangular solid and orient it to the drawing.
What would these shapes look like if we were looking at them from here, in front of a face of the cube or triangular solid?
Many should be able to see it would just be a square or triangle.
Draw a square on the board. How can I make this square look like it is three-dimensional? Hopefully they will say you need to give it some kind of depth. Extend its sides outward and then connect them again in a square until you have a cube.
What is this shape called?
Hold up a wooden cube block and orient it to the drawing. Draw a triangle and repeat the depth idea until there is a triangular solid. Hold up a wooden triangular solid and orient it to the drawing.
What would these shapes look like if we were looking at them from here, in front of a face of the cube or triangular solid?
Many should be able to see it would just be a square or triangle.
 Encourage everyone to try making three dimensional shapes on paper in front of them.
How does light see three dimensional shapes? Can we even try to model that?
Encourage everyone to try making three dimensional shapes on paper in front of them.
How does light see three dimensional shapes? Can we even try to model that?
Have teams of three or more people pick a large and solid shape from a selection of shapes. Give these instructions to the students. Place the blocks on big sheets of paper and trace their position. (Note: This can lead into or follow a multiplication exercise.) Take 35 pipe cleaners, tape each one by an end to the front of a covered textbook, forming a neat 5 x 7 grid pattern. An array of pipe cleaners should now be sticking straight out from the textbook, making the book look like a big hairbrush. Have one student aim the pipe cleaners on the book from some angle above and to the side of the block. They may want to measure the height of the book above the desk top.
What is this representing? What are the pipe cleaners supposed to be?
Have them move the book along in the direction the pipe cleaners point until they hit the paper and the block. Any pipe cleaners that hit the block can be bent back out of the way, while the other pipe cleaners reach past the block to the paper. Tape the pipe cleaner ends to the paper or block where they hit. Move around the class to make sure every team and/or student understands the procedure. One student should carefully trace and darken the area where there are no pipe cleaners touching the paper.
What is this area called? What is the shape?
Teams with triangular solids, for example, will find that their pipe cleaner shadows are very rectangular.
Why is this?
Can any of the groups explain what they are seeing happening here?
Urge them to think about 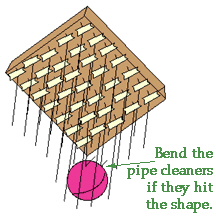 what the shape "looks like" to light.
Can you close one eye and peer at the shapes and see the projection effect? If light really does travel in straight lines, then these shadows are correct. How could we be sure?
Get a bright portable lamp and place it at the same height the book was. Don't turn it on yet. Slide the lamp in front of the block, still at the same height as the book.
What shadow did it make? Is it the same shape shadow as the pipe cleaners made?
what the shape "looks like" to light.
Can you close one eye and peer at the shapes and see the projection effect? If light really does travel in straight lines, then these shadows are correct. How could we be sure?
Get a bright portable lamp and place it at the same height the book was. Don't turn it on yet. Slide the lamp in front of the block, still at the same height as the book.
What shadow did it make? Is it the same shape shadow as the pipe cleaners made?
What if the light were coming from directly on top of the block? Move the lamp above it.
They will see there is little to no shadow.
Where is the shadow? Does anyone lift the block to see the shadow below? Remember, to have a shadow, you need a light, a blocker, and something to cast the shadow on.
What is the shape of the world?
Hold up a sphere.
What kind of shadow would this make? When light rays hit it, what shape do they make?
Students should be able to see they make a circular shadow. Move the ball to a different orientation, which won't look very different.
Now what kind of shadow will be made? The same.
What about in space? Is there anything the shadows can land on? Does the Earth have a shadow? Is there a light, the Sun? Is there a blocker, the Earth? Where could the shadow fall? What else is out there? Many will suggest the Moon or other planets. So, the Earth makes a circular shadow. If this is true, the world would make a circular shadow on the Moon sometimes.
If there is a lunar eclipse happening soon, this would be a great introduction to eclipses. Otherwise, locate eclipse photographs to show them some pictures of a real eclipse.
What is the shape? It is definitely circular. How long does an eclipse take? Hours. What does the Earth do in a few hours of time? It spins. So, if the Earth were a flat circle that spins, would it always cast a round shadow during the eclipse. What does that mean about the shape of our world? Cool.
There is a diagram showing how the phases of the Moon occur. It is important to know that they are not caused by the Earth's shadow.
 There are several basic shapes in our world which show up time and again. We call these the regular solids because their construction is from simple shapes like circles, triangles, and rectangles. To make one of these shapes is to imagine a triangle, say, sitting flat on the table as if cut out from a piece of paper. Flat as it is, it is nearly two-dimensional. What if you could give it height? Imagine being able to grab hold of the three sides and stretch them upwards. From
There are several basic shapes in our world which show up time and again. We call these the regular solids because their construction is from simple shapes like circles, triangles, and rectangles. To make one of these shapes is to imagine a triangle, say, sitting flat on the table as if cut out from a piece of paper. Flat as it is, it is nearly two-dimensional. What if you could give it height? Imagine being able to grab hold of the three sides and stretch them upwards. From  above, it would still look like a triangle, but from the sides, it would look like a building with three sides. This is called a triangular solid. The same technique is used to make a cube or cylinder. These shapes are often called "prisms", but are quite unlike rainbow prisms, so we should not refer to these shapes as such. Instead, they are rectangular solids, because a shadow cast from the long side is always a rectangle.
above, it would still look like a triangle, but from the sides, it would look like a building with three sides. This is called a triangular solid. The same technique is used to make a cube or cylinder. These shapes are often called "prisms", but are quite unlike rainbow prisms, so we should not refer to these shapes as such. Instead, they are rectangular solids, because a shadow cast from the long side is always a rectangle.
 Understanding how light hits things of different shape and form necessitates an understanding of shape and form. Becoming familiar with the shapes around us and having a language to talk about them helps us when we describe other things which are happening in our world. The National Science Education Standards suggest introducing the rectangular solids in elementary school and the manipulation of shapes and perspectives throughout the school year. Older students will benefit from the application of math skills to shape and structure. Vocabulary words which can be introduced to help us talk about our experiences are shapes, edges, sides, cylinder, sphere, triangular solid, rectangular solid, cone, pyramid, and cube.
Understanding how light hits things of different shape and form necessitates an understanding of shape and form. Becoming familiar with the shapes around us and having a language to talk about them helps us when we describe other things which are happening in our world. The National Science Education Standards suggest introducing the rectangular solids in elementary school and the manipulation of shapes and perspectives throughout the school year. Older students will benefit from the application of math skills to shape and structure. Vocabulary words which can be introduced to help us talk about our experiences are shapes, edges, sides, cylinder, sphere, triangular solid, rectangular solid, cone, pyramid, and cube.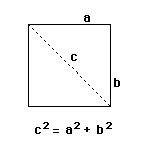 Thinking about the way light hits objects is a good way of thinking about the geometry of these solids. In math, we say that the length of the diagonal cut across the face of a square, let's call it "c", is equal to the square root of the squared lengths of the two sides, a and b. This means that the diagonal is longer than the sides by a little bit. You can find this out yourself with shadows cast on a rectangular solid. If the light is aimed at a side of the solid, the shadow will be a certain width.
Thinking about the way light hits objects is a good way of thinking about the geometry of these solids. In math, we say that the length of the diagonal cut across the face of a square, let's call it "c", is equal to the square root of the squared lengths of the two sides, a and b. This means that the diagonal is longer than the sides by a little bit. You can find this out yourself with shadows cast on a rectangular solid. If the light is aimed at a side of the solid, the shadow will be a certain width.  However, if the solid is turned slightly so that the light is aimed at a corner, the shape of the shadow will still be slightly wider than before. This is the nature of the projection effect of shadows cast from different angles of a rectangular solid.
However, if the solid is turned slightly so that the light is aimed at a corner, the shape of the shadow will still be slightly wider than before. This is the nature of the projection effect of shadows cast from different angles of a rectangular solid.
 Download
Download
 For Kindergarten through second grade, this Thread focuses on manipulating shapes and sorting objects. This is a great exercise for this age group. They are quite capable of sorting by size and are learning about classification. Geometrical classification by shadow casting may be a bit too complex for them, because children at this age tend to find hierarchical categories confusing. In part because, they tend to assume that categories are mutually exclusive! Superordinate categories create the most difficulty.
For Kindergarten through second grade, this Thread focuses on manipulating shapes and sorting objects. This is a great exercise for this age group. They are quite capable of sorting by size and are learning about classification. Geometrical classification by shadow casting may be a bit too complex for them, because children at this age tend to find hierarchical categories confusing. In part because, they tend to assume that categories are mutually exclusive! Superordinate categories create the most difficulty.
 Let's play with shapes in the light to get a feel for shadows of shapes.What is a cube? Which of these shapes are round in some way? How could you sort these objects into groups? What are some things about these shapes that make them different from other shapes? What names would you give for these shapes?
Let's play with shapes in the light to get a feel for shadows of shapes.What is a cube? Which of these shapes are round in some way? How could you sort these objects into groups? What are some things about these shapes that make them different from other shapes? What names would you give for these shapes?
 A tabletop full of geometric solids and their flat counterparts is a good visual. If there are enough shapes, one set at each group table would be great. How could we sort this group? Students may find links between the triangle and the pyramid or the cone and the pyramid.
Can anyone explain why they made the grouping that they did? What does the group look like when placed on the overhead projector? Is there a way of making a group on the overhead projector whose shadows look alike?
A tabletop full of geometric solids and their flat counterparts is a good visual. If there are enough shapes, one set at each group table would be great. How could we sort this group? Students may find links between the triangle and the pyramid or the cone and the pyramid.
Can anyone explain why they made the grouping that they did? What does the group look like when placed on the overhead projector? Is there a way of making a group on the overhead projector whose shadows look alike? 



 hape that is sitting there from the projection. It may be hard to figure it out because of how sometime two very different shapes can make similar shadows. Ask them which shape this could be and why. For example, a triangular solid sitting lengthwise on the projector table will look like a rectangle. Ask them what they could do to be really sure of what the shape was, besides moving the blocking screen you have constructed? They will hopefully say to rotate the object or turn it over on the projector table. A triangle will show up, and then it is obvious. Lift the shape so everyone sees it and go to the next.
hape that is sitting there from the projection. It may be hard to figure it out because of how sometime two very different shapes can make similar shadows. Ask them which shape this could be and why. For example, a triangular solid sitting lengthwise on the projector table will look like a rectangle. Ask them what they could do to be really sure of what the shape was, besides moving the blocking screen you have constructed? They will hopefully say to rotate the object or turn it over on the projector table. A triangle will show up, and then it is obvious. Lift the shape so everyone sees it and go to the next.


 Encourage everyone to try making three dimensional shapes on paper in front of them.
How does light see three dimensional shapes? Can we even try to model that?
Encourage everyone to try making three dimensional shapes on paper in front of them.
How does light see three dimensional shapes? Can we even try to model that? what the shape "looks like" to light.
Can you close one eye and peer at the shapes and see the projection effect? If light really does travel in straight lines, then these shadows are correct. How could we be sure?
Get a bright portable lamp and place it at the same height the book was. Don't turn it on yet. Slide the lamp in front of the block, still at the same height as the book.
What shadow did it make? Is it the same shape shadow as the pipe cleaners made?
what the shape "looks like" to light.
Can you close one eye and peer at the shapes and see the projection effect? If light really does travel in straight lines, then these shadows are correct. How could we be sure?
Get a bright portable lamp and place it at the same height the book was. Don't turn it on yet. Slide the lamp in front of the block, still at the same height as the book.
What shadow did it make? Is it the same shape shadow as the pipe cleaners made? 