


Next: Windowing
Up: Period Determination
Previous: Periodogram
One major
advantage of the periodogram method is that it generates a value called
the power. The power can be converted to the probability
that the period found is not true, the false alarm probability (FAP).
Scargle (1982) showed that the probability distribution returned by
this method is exponential, and thus the probability of a false alarm
is defined as 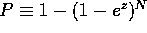 , where z is the power at a
given frequency and N is the number of frequencies sampled.
Unfortunately, the formulation for calculating the FAP is
only valid in the case where the data are not clumped in their sampling.
The data reported here are clumpy since up to four observations are taken
per night, but none during the day.
, where z is the power at a
given frequency and N is the number of frequencies sampled.
Unfortunately, the formulation for calculating the FAP is
only valid in the case where the data are not clumped in their sampling.
The data reported here are clumpy since up to four observations are taken
per night, but none during the day.
To overcome this problem, Eaton et al. (1995) have suggested calculating the
power of the most likely period in a set of data created by randomizing
the night number associated with observations of a given star. By
calculating the maximum power on a large number of randomized data,
the conversion from power to FAP can be individually determined for each
set of observations in a statistical manner.
However, it is still possible to have several possible periods with
less than 1% probability of being true.
This is due to aliasing in the dataset.
Aliasing is caused by periodicity in the timing observations being
coupled with the periodic nature of the source.
The sampling theorem shows that if the frequency of a
continuous function 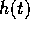 (in this case the amplitude) is less than half the
sampling frequency (the Nyquist frequency) the original signal can be
recovered. Given a sampling time interval
(in this case the amplitude) is less than half the
sampling frequency (the Nyquist frequency) the original signal can be
recovered. Given a sampling time interval 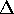 , one can identify
individual observations at time t as the
, one can identify
individual observations at time t as the 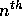 observations.
If one were to observe an infinite number of times, one would obtain:
observations.
If one were to observe an infinite number of times, one would obtain:
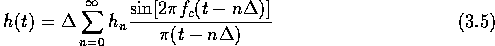
where:  is the Nyquist frequency.
This has an unfortunate side effect, Two waves,
is the Nyquist frequency.
This has an unfortunate side effect, Two waves, 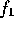 and
and 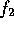 give
the same samples if they differ by 1/
give
the same samples if they differ by 1/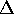 .
This implies than any given sample can be
reconstructed into an infinite number
of original signals all separated by n/
.
This implies than any given sample can be
reconstructed into an infinite number
of original signals all separated by n/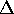 in frequency space.
Any power in the
spectral density which exists outside the search range is moved into the
search range. Two periods p1 and p2
will give the same samples, and thus be indistinguishable,
if they differ by the inverse of the sampling
frequency. The problem is complicated by the two sampling frequencies
in the data, the diurnal cycle and the
in frequency space.
Any power in the
spectral density which exists outside the search range is moved into the
search range. Two periods p1 and p2
will give the same samples, and thus be indistinguishable,
if they differ by the inverse of the sampling
frequency. The problem is complicated by the two sampling frequencies
in the data, the diurnal cycle and the 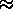 three hours between
samples each night. The aliasing causes
several peaks in the periodogram analysis to appear at similar power.
three hours between
samples each night. The aliasing causes
several peaks in the periodogram analysis to appear at similar power.



Next: Windowing
Up: Period Determination
Previous: Periodogram
Scott J. Wolk
Thu Dec 5 11:30:29 EST 1996
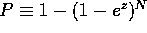 , where z is the power at a
given frequency and N is the number of frequencies sampled.
Unfortunately, the formulation for calculating the FAP is
only valid in the case where the data are not clumped in their sampling.
The data reported here are clumpy since up to four observations are taken
per night, but none during the day.
, where z is the power at a
given frequency and N is the number of frequencies sampled.
Unfortunately, the formulation for calculating the FAP is
only valid in the case where the data are not clumped in their sampling.
The data reported here are clumpy since up to four observations are taken
per night, but none during the day.
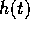 (in this case the amplitude) is less than half the
sampling frequency (the Nyquist frequency) the original signal can be
recovered. Given a sampling time interval
(in this case the amplitude) is less than half the
sampling frequency (the Nyquist frequency) the original signal can be
recovered. Given a sampling time interval 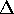 , one can identify
individual observations at time t as the
, one can identify
individual observations at time t as the 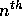 observations.
If one were to observe an infinite number of times, one would obtain:
observations.
If one were to observe an infinite number of times, one would obtain:
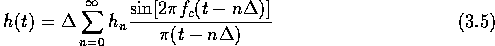
 is the Nyquist frequency.
This has an unfortunate side effect, Two waves,
is the Nyquist frequency.
This has an unfortunate side effect, Two waves, 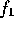 and
and 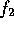 give
the same samples if they differ by 1/
give
the same samples if they differ by 1/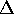 .
This implies than any given sample can be
reconstructed into an infinite number
of original signals all separated by n/
.
This implies than any given sample can be
reconstructed into an infinite number
of original signals all separated by n/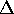 in frequency space.
Any power in the
spectral density which exists outside the search range is moved into the
search range. Two periods p1 and p2
will give the same samples, and thus be indistinguishable,
if they differ by the inverse of the sampling
frequency. The problem is complicated by the two sampling frequencies
in the data, the diurnal cycle and the
in frequency space.
Any power in the
spectral density which exists outside the search range is moved into the
search range. Two periods p1 and p2
will give the same samples, and thus be indistinguishable,
if they differ by the inverse of the sampling
frequency. The problem is complicated by the two sampling frequencies
in the data, the diurnal cycle and the 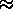 three hours between
samples each night. The aliasing causes
several peaks in the periodogram analysis to appear at similar power.
three hours between
samples each night. The aliasing causes
several peaks in the periodogram analysis to appear at similar power.