
The other period search technique is the periodogram which is based on the prescriptions of Lomb (1976) and Horne & Balinas (1986). The periodogram is essentially a discrete Fourier transform of the input data. Any function of time can be written as a function of frequency:

This transformation conserves power:
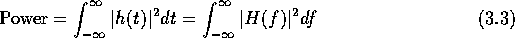
Decomposition of a regularly sampled signal into its Fourier components is straightforward. The difficulty that arises in astronomical data is that weather and daylight usually render even sampling impossible. The classical periodogram is defined as a discrete sum:
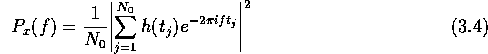
The periodogram provides an approximation to the power spectrum. In this respect, the procedure breaks down the signal into sine wave components across a frequency range. The residuals of the least squares fit to the data are then summed. The period is chosen by minimization of this sum.