Mexican Hat [EotW]
The most widely used tool for detecting sources in X-ray images, especially Chandra data, is the wavelet-based wavdetect, which uses the Mexican Hat (MH) wavelet. Now, the MH is not a very popular choice among wavelet aficianados because it does not form an orthonormal basis set (i.e., scale information is not well separated), and does not have compact support (i.e., the function extends to inifinity). So why is it used here?
The short answer is, it has a convenient background subtractor built in, is analytically comprehensible, and uses concepts very familiar to astronomers. The last bit can be seen by appealing to Gaussian smoothing. Astronomers are (or were) used to smoothing images with Gaussians, and in a manner of speaking, all astronomical images already come presmoothed by PSFs (point spread functions) that are nominally approximated by Gaussians. Now, if an image were smoothed by another Gaussian of a slightly larger width, the difference between the two smoothed images should highlight those features which are prominent at the spatial scale of the larger Gaussian. This is the basic rationale behind a wavelet.
So, in the following, G(x,y;σx,σy,xo,yo) is a 2D Gaussian written in such that the scaling of the widths and the transposition of the function is made obvious. It is defined over the real plane x,y ε R2 and for widths σx,σy. The Mexican Hat wavelet MH(x,y;σx,σy,xo,yo) is generated as the difference between the two Gaussians of different widths, which essentially boils down to taking partial derivatives of G(σx,σy) wrt the widths. To be sure, these must really be thought of as operators where the functions are correlated with a data image, so the derivaties must be carried out inside an integral, but I am skipping all that for the sake of clarity. Also note, the MH is sometimes derived as the second derivative of G(x,y), the spatial derivatives that is.
The integral of the MH over R2 results in the positive bump and the negative annulus canceling each other out, so there is no unambiguous way to set its normalization. And finally, the Fourier Transform shows which spatial scales (kx,y are wavenumbers) are enhanced or filtered during a correlation.
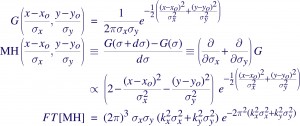
hlee:
There was an arxiv paper related to your title: Asymptotic Uncorrelation for Mexican Needlets by Azita Mayeli
06-19-2008, 6:18 pm