
This is
a Stickup!
 In this Thread, we are continuing to examine the passage of time from observations we can make about the outside world. In Hello, Sun!, we saw that the Sun appears to jog across the sky during the school day. It looks like a nice and smooth motion. By using the shadow of the Sun during the day, we may make safe and accurate measurements of that motion. The National Standards require that students be learning what causes light, heat and shadow, and how time passes, how to use rulers and other measuring tools. The vocabulary words which can be introduced to help us talk about our experiences are line, length, angle, sphere, straight, and model.
In this Thread, we are continuing to examine the passage of time from observations we can make about the outside world. In Hello, Sun!, we saw that the Sun appears to jog across the sky during the school day. It looks like a nice and smooth motion. By using the shadow of the Sun during the day, we may make safe and accurate measurements of that motion. The National Standards require that students be learning what causes light, heat and shadow, and how time passes, how to use rulers and other measuring tools. The vocabulary words which can be introduced to help us talk about our experiences are line, length, angle, sphere, straight, and model.

 We
have already explored the way the Sun moves in the sky during the day. The next step is to try and see that motion from another perspective. Some classes may have been able to determine the height of the Sun in fists and found that the Sun first gets higher then lower in the sky. Did students also notice that their shadows got shorter and then longer again? Do they have a record of that? As we saw from the Thread, Me and My Shadow, the height of a light source changes the lengths and orientations of shadows. Using a standard stick with careful measurements can give us a better record of the changing shadow lengths outside in the Sun and also good data for exploring deeper.
We
have already explored the way the Sun moves in the sky during the day. The next step is to try and see that motion from another perspective. Some classes may have been able to determine the height of the Sun in fists and found that the Sun first gets higher then lower in the sky. Did students also notice that their shadows got shorter and then longer again? Do they have a record of that? As we saw from the Thread, Me and My Shadow, the height of a light source changes the lengths and orientations of shadows. Using a standard stick with careful measurements can give us a better record of the changing shadow lengths outside in the Sun and also good data for exploring deeper.
If we measure shadow lengths during the day using a standard stick, the shadow pattern will look like a fan of lines, first long, then shorter, then long again. This fan will begin with its first shadow line on the left of the stick, if you are looking from South of the stick This fan pattern will then proceed with lines moving ever more to the right and at steeper angles to the edge of the paper. This is because the Sun rises in the East, or to the right of the stick. A light source on the right will cast a shadow of an object to the left. The angle of the Sun above the horizon determines the length of the shadows it causes behind objects. The higher the Sun is, the shorter the shadow. This is why the fan gets shorter at mid-day. In fact, if the Earth did not tilt on its axis 23.5° as it does, then the Sun's height at mid-day would be the same every day of the year. The Thread called Latitudes and Attitudes will let us explore this further.
At one point in the investigation, you will talk about the relationship between angles and sides of a right triangle. A right triangle is one which has a 90° angle in it. In such a triangle, the tangent of an angle is defined as the length of the side opposite the angle divided by the length of the side next to the angle. The hypotenuse, or longest side, is not used in finding the tangent. In the sunstick investigation, the tangent of the angles use the "sides" made by the length of the stick and the length of the shadow. So, depending on which angle you are trying to find, you will divide one by the other. In a calculator or using a table of tangents, you can find the angle. In the upper grades, you will use a protractor and some string to measure the angles directly as well as finding them with the tangent.
If you are interested in making sundials with your class, please check out this pattern for a simple design for a sundial.

 This age group cannot yet manage the precision required for the Investigation in this Thread. They will not be able to make good measurements nor understand their importance. What we want them to learn from this adventure is that as it moves across the sky, the Sun's light changes the stick's shadow, something which they should remember from Me and My Shadow. However, we can emphasize using the Sun as a clock in this Thread. It is suggested that instead of employing the measuring stick and paper that you instead use a sapling or pole in the school yard and bright marking objects or flags. This way we can express the same basic concept in a very big and personal way, using first our bodies to mark where the shadows are and then special flags we place to make semi-permanent records of the shadows. Decorating personal flags would be a fine integration of art into this Thread for this age group.
This age group cannot yet manage the precision required for the Investigation in this Thread. They will not be able to make good measurements nor understand their importance. What we want them to learn from this adventure is that as it moves across the sky, the Sun's light changes the stick's shadow, something which they should remember from Me and My Shadow. However, we can emphasize using the Sun as a clock in this Thread. It is suggested that instead of employing the measuring stick and paper that you instead use a sapling or pole in the school yard and bright marking objects or flags. This way we can express the same basic concept in a very big and personal way, using first our bodies to mark where the shadows are and then special flags we place to make semi-permanent records of the shadows. Decorating personal flags would be a fine integration of art into this Thread for this age group.
 What is happening to the Sun outside during the day? Is it staying in one place? Does it seem to move? What happens to our shadows if the light moves? Do you think our sunlight shadows could move, too? What if we move? Do our shadows move with us? Does the Sun/Blocker/Shadow game work if we move? How could we try it out? How long would it take before we noticed any movement? Can we actually see the Sun moving? How long did it take in Hello, Sun! before we noticed the motion?
What is happening to the Sun outside during the day? Is it staying in one place? Does it seem to move? What happens to our shadows if the light moves? Do you think our sunlight shadows could move, too? What if we move? Do our shadows move with us? Does the Sun/Blocker/Shadow game work if we move? How could we try it out? How long would it take before we noticed any movement? Can we actually see the Sun moving? How long did it take in Hello, Sun! before we noticed the motion?
 Arrange ahead of time for your observation place to be undisturbed by students during the day and recess. Perhaps alerting your principal about the activity will help.
Outside, let's pick a short tree or pole (or use a standard stick) on which the school's shadow does not fall anytime during the day. It would be best if this object were near the place where we all did Hello, Sun! so similar horizon landmarks are around us. This will help us understand what is going on.
Arrange ahead of time for your observation place to be undisturbed by students during the day and recess. Perhaps alerting your principal about the activity will help.
Outside, let's pick a short tree or pole (or use a standard stick) on which the school's shadow does not fall anytime during the day. It would be best if this object were near the place where we all did Hello, Sun! so similar horizon landmarks are around us. This will help us understand what is going on.
What time is it? Where is the shadow of our tree? Can we all go run to the shadow and stand on it? How long is the shadow? Could someone go stand at the very end of the shadow?
Place a little class flag there with the time written on it.
Who thinks the shadow will be somewhere else in an hour? Where? Stand on the spot you think it will be. With our names on our own flags (of a different color than the class flag), let's each place a flag down where each of us thinks the shadow will be in one hour.
Pick random students' flags and ask them why they chose that spot. Could they relate their decision to the Sun at all?
Where do we think the Sun will be in one hour?
In one hour, go outside again.
Where is the end of the shadow? Mark this with another class flag. Who was closest? Which way did the shadow move? What is changing? Where is the Sun? Did the tree shrink or grow? Let's retrieve our personal flags. Where might the shadow be next hour?
This time students may begin to see that a pattern might be forming, and many will put their flag to the right of the second class flag. Again, ask them why and if they can relate it to the Sun.
By the third hour out, it should be clear what is happening to the pattern of the shadow. It is moving to the right. The length of the shadow is not going to make much sense to them, since it involves the height of the Sun; pointing out the correlation will be difficult. However, with flashlights inside, repeating the You Light Up my Life investigation may allow more modeling of the situation. Consider this if you feel your students might gain insight. Otherwise, it is not crucial at this age group. These are understandings they can build as they get older.
Which way did the Sun go today? Which way did the shadow go? Did the tree move at all during the day? No ... so what happened?
Play the Sun/Blocker/Shadow game again inside with a flashlight, some object, and paper. Model the experience from outside with everyone. Ask them every step of the way if this is where the Sun was and this is where the tree or pole was.
Which way did the shadow go? Is the Sun going that way? Does it happen like that for everyone in the whole world?

 This is a good Thread for this age group. They are beginning to learn about numbers and how to use measuring tools. At this age they are extra keen not to make mistakes, since they are desperate to fit in and avoid looking stupid. And they want to be given real tasks to do. These characteristics make a subset of this Thread perfect for your students. We will not delve into this situation's geometry with these students, but we will let them participate in some serious observing, building, and modeling in a way which we hope will satisfy their intellectual desires.
This is a good Thread for this age group. They are beginning to learn about numbers and how to use measuring tools. At this age they are extra keen not to make mistakes, since they are desperate to fit in and avoid looking stupid. And they want to be given real tasks to do. These characteristics make a subset of this Thread perfect for your students. We will not delve into this situation's geometry with these students, but we will let them participate in some serious observing, building, and modeling in a way which we hope will satisfy their intellectual desires.
 How does the Sun seem to move during the day? From where to where? Recall the Hello, Sun! blackboard drawings? Could anyone draw them on the board? So, since we were facing South, the Sun moved from left to right. What happens to shadows made by the Sun during the day, then? How could we observe them and be able to take them inside to look at? Can we take somebody else's shadows inside? How could we do this?
Gather suggestions from them. Many will recall that we were able to take the Hello, Sun! data indoors because we made a record of it.
How could we make a record of the shadows? They will suggest putting paper on the ground, perhaps, or taking pictures. Will one picture be able to show us all of the shadows from a whole day? No. A piece of paper would work, if it had all of the shadows on it. How big a piece of paper? How long are shadows? And what should we use as a shadow maker?
How does the Sun seem to move during the day? From where to where? Recall the Hello, Sun! blackboard drawings? Could anyone draw them on the board? So, since we were facing South, the Sun moved from left to right. What happens to shadows made by the Sun during the day, then? How could we observe them and be able to take them inside to look at? Can we take somebody else's shadows inside? How could we do this?
Gather suggestions from them. Many will recall that we were able to take the Hello, Sun! data indoors because we made a record of it.
How could we make a record of the shadows? They will suggest putting paper on the ground, perhaps, or taking pictures. Will one picture be able to show us all of the shadows from a whole day? No. A piece of paper would work, if it had all of the shadows on it. How big a piece of paper? How long are shadows? And what should we use as a shadow maker?
Look around the room and find a standard stick.
How could we keep this stick from falling over?
A can with junk in it to keep the stick still is a good idea: things like clay and rocks, a Styrofoam plant basket block and stones, or a coffee can filled with sand are good ideas. Paper from a big roll and masking tape will be good for the record keeping. And a nice new marker.
 Time the observations to coincide with the times we all went out for Hello, Sun! Bring all of the materials outside. Find the location from Hello, Sun! and put your equipment down there. Pull out a large sheet (about four feet long and as wide as the paper itself) and lay it down with one corner pointing towards south. (Human symmetry ideals would want you to put it square with a side facing south. Don't give in. Since the shadows at morning will be longer than those in mid-day, you will need to account for this in the orientation of your paper.) Tape the paper very firmly down. You may want to mark where the edges of the paper are in case it blows out of position. Put the can down in the corner. Make a careful circle around the bottom of the can so that you always know where it is supposed to go.
Time the observations to coincide with the times we all went out for Hello, Sun! Bring all of the materials outside. Find the location from Hello, Sun! and put your equipment down there. Pull out a large sheet (about four feet long and as wide as the paper itself) and lay it down with one corner pointing towards south. (Human symmetry ideals would want you to put it square with a side facing south. Don't give in. Since the shadows at morning will be longer than those in mid-day, you will need to account for this in the orientation of your paper.) Tape the paper very firmly down. You may want to mark where the edges of the paper are in case it blows out of position. Put the can down in the corner. Make a careful circle around the bottom of the can so that you always know where it is supposed to go.
So that we don't all crowd the paper with our shadows, let's stand on the north side of the paper.
(There is no need to call things north and south with this age group. They will get all fuddled up with the vocabulary. You might say, "Let's stand at the top of the paper.")
What time is it? Someone look at a watch. Where is the shadow here?
Trace the shadow line carefully with a dark marker. Write the time at the shadow's end. (Do this for every shadow observation today. Putting the date down near the bottom of the paper is probably a good idea.)
The shadow is to our right. Where is the Sun? It is to our left. How long is this shadow? Where do we think the shadow will be in one hour? Does anyone recall Hello, Sun! and what we learned about how the Sun moved in the course of one hour? What might that do to the shadow? Will the Sun be higher in the sky? What might that do to the shadow?
The students may want to place stones on the paper marking where they think the next shadow will be. If they think the shadow might change size, they should place their stone where they think the end of the shadow will be.
 Back outside again in one hour ... where did the shadow move? How many things outside in our set-up could be changing? Let them decide if the stick could have changed size. Could the paper have changed size? What else is changing? Where is the Sun? (Remember not to look at directly at the Sun, as that may cause permanent damamge to the eye's retina.) Is there a connection? How long is the shadow? Where in the sky is the Sun?
Back outside again in one hour ... where did the shadow move? How many things outside in our set-up could be changing? Let them decide if the stick could have changed size. Could the paper have changed size? What else is changing? Where is the Sun? (Remember not to look at directly at the Sun, as that may cause permanent damamge to the eye's retina.) Is there a connection? How long is the shadow? Where in the sky is the Sun?
Back in the classroom, retrieve the Hello, Sun! easel drawing. Leave it in view during this day as a reference guide for students.
What time did we make this last observation? Can anyone find it on the Hello, Sun! drawing? How high is the Sun now as compared to one hour ago? Did anything happen to the shadow during this last hour? What might be the link?
They may or may not see the height and length relationship right away, so encourage more thinking until they propose the idea. When they do, ask them when they think the shadow might be the shortest today, or when it will be the longest. If they do not see the connection yet, revisit this line of questioning after each observation outside until they do.
After a completed sun stick record has been made (i.e. at the end of the day) tape the record up in the classroom.
Tomorrow we will be thinking more about this day and building our own models of it.
The next day, set aside a table for the flashlight/toothpick/clay/paper materials and begin talking with the class about our experiences from the previous day.
What did we do yesterday and what do we think we have discovered? We think we discovered that as the Sun moved across the sky and up and down in the sky, the shadows moved across the paper and got longer or shorter. How could we try to model that inside the classroom? We would need a Sun, right? What if we wanted everyone to have his own Sun? What could we use instead of a Sun? What is the Sun anyway?
They should hopefully recall their experiences with You Light Up My Life well enough to know that light is light, whatever its source, and that objects in the path of flashlights will cast shadows just as they do in the path of sunlight.
What else do we need? We need some kind of little stick stuck into something. A toothpick in clay works well. And we need paper and markers. No problem.
In teams of two, have them gather one set of materials and bring them to a desk or table. Can they recreate what happened outside? Give them plenty of time to fiddle with the materials. They will want desperately to play with the flashlights at first, but not as badly as they did in You Light Up My Life. Ask them to focus on recreating the events of yesterday. What must they do with the flashlight to get their toothpick shadows looking like those on yesterday's record taped to the wall? Have them tell you why they built their model the way they did and how they constructed it. Perhaps teams could later come to the front and explain their models to the rest of the class.
What can we see here?
Grab someone's flashlight and aim it down from above the very top of the toothpick.
What kinds of things would happen to the shadows if we did this? There would be no shadow. Does this happen on the Earth anywhere? What about if we really lowered the flashlight (aim it at the side of the toothpick and very low). The shadows would be very long. Does this ever happen on the Earth?
Gather their suggestions. Ask that they write up their experiences from the past few days, especially what they think they learned and what more they might want to learn about how shadows work on the Earth.

 These students are ready to make some serious observations about their world. This age group is able to record data and comprehend the need for careful observation. They are responsible and eager to master skills. The onset of puberty often hampers a child's desire to take risks. The simplicity of the observations and the obvious results as they come in provide a student with a comfortable experience in which to make some important predictions. The journal keeping is a very personal thing and can be a safe, private place also to record their ideas. Modeling our investigation in this Thread will help make some connections between the math we are doing and what it shows about the world around us. At this age group, most curricula are introducing basic geometry: triangles, circles, and some simple concepts associated with them. This Thread uses degrees, fractions, angles and triangles to explore the spin speed of the Earth, the height of the Sun, and later in the year, the tilt of the Earth. It is fairly important that the students be familiar with the protractor before this Investigation. By the time protractors are used in this Investigation, you and your class will be involved in some serious thinking and connection building. It will distract from the cognitive process to stop and learn about the protractor in the middle of the thread.
These students are ready to make some serious observations about their world. This age group is able to record data and comprehend the need for careful observation. They are responsible and eager to master skills. The onset of puberty often hampers a child's desire to take risks. The simplicity of the observations and the obvious results as they come in provide a student with a comfortable experience in which to make some important predictions. The journal keeping is a very personal thing and can be a safe, private place also to record their ideas. Modeling our investigation in this Thread will help make some connections between the math we are doing and what it shows about the world around us. At this age group, most curricula are introducing basic geometry: triangles, circles, and some simple concepts associated with them. This Thread uses degrees, fractions, angles and triangles to explore the spin speed of the Earth, the height of the Sun, and later in the year, the tilt of the Earth. It is fairly important that the students be familiar with the protractor before this Investigation. By the time protractors are used in this Investigation, you and your class will be involved in some serious thinking and connection building. It will distract from the cognitive process to stop and learn about the protractor in the middle of the thread.
 When the Sun moves across the sky, how could we really record its exact position? It is extremely dangerous to look directly at the Sun. How else could we possibly try to record themotion?
Let's hope they are thinking about the Sun as a light source and that they know an awful lot about the characteristics of light sources now. If not, ask them if the Sun is a light. What do they know about light sources?
What can lights do? What results occur when we put something in the way of the light? Is there anything important about the light we can learn from what happens to the shadow of the object in its way? We can tell how bright it is, sometimes, by the darkness of the shadow if the object is very opaque. What about the height of the light? If light travels in straight lines, what happens to a shadow if the light comes from up here?
Aim a pretend flashlight up high above someone's head. This may not be obvious to everyone. Good. That means it is time to go outside and experience this all for ourselves.
When the Sun moves across the sky, how could we really record its exact position? It is extremely dangerous to look directly at the Sun. How else could we possibly try to record themotion?
Let's hope they are thinking about the Sun as a light source and that they know an awful lot about the characteristics of light sources now. If not, ask them if the Sun is a light. What do they know about light sources?
What can lights do? What results occur when we put something in the way of the light? Is there anything important about the light we can learn from what happens to the shadow of the object in its way? We can tell how bright it is, sometimes, by the darkness of the shadow if the object is very opaque. What about the height of the light? If light travels in straight lines, what happens to a shadow if the light comes from up here?
Aim a pretend flashlight up high above someone's head. This may not be obvious to everyone. Good. That means it is time to go outside and experience this all for ourselves.
Let's bring something outside which we know a lot about. Here's a piece of wood (the 12 inch dowel rod or ruler, or the half-meter stick). How long is it? How could we know for sure?
Have them suggest and implement the act of measuring it with a ruler.
OK, so we know it is a foot long. Let's stick this outside and watch its shadows all day and measure them as well.
If they did this kind of thing last year, they may pipe up and say so. Ask them if they ever measured the shadows they made then or if they discovered the speed of the Sun's movement? Well, no. OK, then. Time to roll.
 Bring the easel and paper out again. Outside, with the materials set up in a good sunny spot, have them carefully pin down the paper somewhere safe where it won't be trampled. You might ask them which way is South. Suggest they point a corner of the big paper to the South and put the can with the upright dowel near that corner.
What happens if the can slips? What could we do to make sure we always know where the can goes? What happens if the paper slips? What could we do to make sure we know where the corners of the paper were?
Taping the corners down and chalking the outline of the paper seems to work well. Outline the can on the paper itself. If it is windy, weights on the corners of the paper should be used.
Bring the easel and paper out again. Outside, with the materials set up in a good sunny spot, have them carefully pin down the paper somewhere safe where it won't be trampled. You might ask them which way is South. Suggest they point a corner of the big paper to the South and put the can with the upright dowel near that corner.
What happens if the can slips? What could we do to make sure we always know where the can goes? What happens if the paper slips? What could we do to make sure we know where the corners of the paper were?
Taping the corners down and chalking the outline of the paper seems to work well. Outline the can on the paper itself. If it is windy, weights on the corners of the paper should be used.
What time is it? Where is the shadow?
Have someone trace the shadow with dark marker very very carefully.
Why so carefully? When we measure, we need to have a good record.
Mark the time of the traced shadow at the top of the traced line.
We might all make some guesses as to where we think the shadow might be next time we come out to check our set-up by placing rocks or sticks on the paper.
Where is the Sun?
Have a team draw the horizon on the easel as seen from the spot in front of the stick (i.e. the sky's southern hemisphere).
In that case, what might we want to know about where we are standing with the easel?
Have them make some mark on the ground so that they can stand in the same place again after one hour. Ask them to draw the Sun in, using the "fists" technique from Hello, Sun!
Where will the Sun be in an hour?
They will point to some spot on the paper.
Let's keep this drawing going along with the sun stick record. So, where might the shadow be after the Sun has moved for an hour? And the length of the shadow? Longer, shorter, or the same? Why?
Gather ideas but don't encourage any one over another. We'll soon see in an hour!
In one hour, revisit the set-up.
Before we trace the shadow, what might we want to do?
Check that everything is in its place. Then have someone trace the shadow carefully, marking the time at the top of the shadow line again.
So, what happened here? Tell me about how the new shadow is changed from the last one.
Someone will tell you that it moved and that it got shorter.
Why did it do this? Did the stick move or get shorter? What is the only thing that can change the shadow? The light. So, the light moved in some way. Where is the Sun now?
Have the Sun keepers stand in their spot and draw the Sun in on the easel.
Is there a connection?
If no one sees that when the Sun moves to the right, the shadow moves to the left, that is fine. We can just keep saying these things.
Also, how many "fists" high is the Sun? How long is the shadow? What is happening here?
Each successive visit outside will become less interesting to them until past midday (when the Sun reached its highest point in the sky) when the shadows get longer again.
Why is this happening? Do we now make the connection? How could we model that inside the classroom?
They should think about this for tomorrow, for we will be building our own models then and discovering some things about the world from them. For homework, you may have them write in their journals what they think happens during the day to shadows and the Earth and Sun. Can they imagine what shadows would be like somewhere else on the Earth? Before they arrive for the next day, tape the easel drawings to the wall above the sun stick drawing (in the diamond orientation).
The next day, ask them what happened yesterday and what they think they now know. Show them that you put up the drawings we made so that they are just like they were when we saw them on the ground. Have them think about (but not call out) the two positions the drawings have been in.
Break the students into teams of four people, hand out the sets of sun-stick models (flashlight/toothpick/clay/paper) and have the teams rebuild the set-ups.
How can we recreate the scene with flashlights? Where did the Sun come up this morning? Where did it go and how high? When were the shadows the longest? The shortest? What is the real connection? Have them tell you what they think is happening.
They will say things like, "When the Sun is highest, the shadows are shortest." Ask them why.
Does it have to do with the nature of light? Can anyone draw what is happening in their model or outside on the board?
Help by drawing the stick in the middle and put the Sun on the far left. Ask someone to come up and draw how the light is coming to the stick. Ask the class where the shadow is. They will want to come up and point or draw it in. Extend the sunlight lines past the very tip top of the stick line (if they are not past it already) so that they reach beyond and mark the end of the shadow. Ask them about shadows again and what they learned from You Light Up my Life if they wonder why you are asking that. Flashbacks are no problem, and are always encouraged. When everyone understands, draw the Sun higher and over more to the right. Have someone else come up and draw how the light is coming to the stick. Where is the shadow now? And so on.
Tape to the board next to the chalk drawings (but higher up) the easel drawing of the Sun. Underneath this, tape the sun stick drawings for comparison.
Is this what we saw? Yes. What has happened is that we have experienced something and set it aside. We then modeled it and thought about it in lines and direction, and set this next to our first experience. What was true for one is true for the other, and vice versa. Since these two experiences support each other, each view is as valid as the other.
The 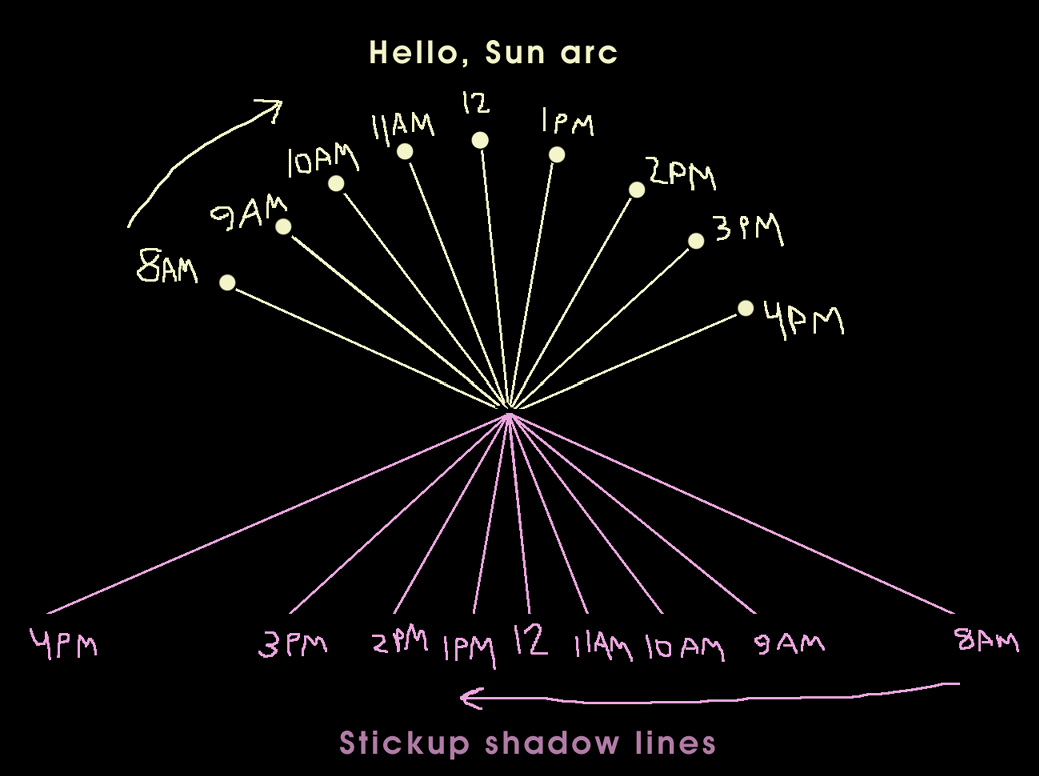 next step is taking a trip to the third realm of experience: the mathematical one.
How could we communicate our experience in terms of mathematical models?
next step is taking a trip to the third realm of experience: the mathematical one.
How could we communicate our experience in terms of mathematical models?
Isolate one section of the chalk drawing on the board (by either erasing the rest or re-drawing the key parts) so that it looks like a little triangle formed from the sunlight line zooming past the top of the stick, the sun stick itself, and the line marking where the shadow was cast.
What shape is this? A triangle. What do you know about triangles? What does the word itself say to you? Tri = Three, angle = some height measured in degrees. Point back to the drawing on the board. Which angle opens up and points to the Sun's position?
Draw a Sun high on the board. Ask some class members where the stick's shadow would be on their model if this Sun could give off light?
How could we test this?
Hopefully, they will use the flashlight in their hands and move them so that they are in line with the Sun mark without leaving their desks.
So, how high is the flashlight or the Sun mark above the paper in degrees?
Trace the line from the Sun to the end of the shadow--but with what?
It would be good to trace the length of the shadow with a pencil first. Then, have one person hold the flashlight while another holds a string to the flashlight near the lens. A third person should pull the string until the other free end reaches the tip of the shadow drawn on the paper.
What is the shape made by the string, the toothpick, and the paper shadow outline?
The fourth person should be able to see this shape by viewing the whole construction from the side.
What does the string represent? It points to the Sun. It follows that an angle formed at the corner by the string and the paper "ground", represents the "Sun's" angle above the ground. Can the fourth person see how this is possible by tracing with his or her eye the line made by the string up to the "Sun"? Can she explain it to everyone else in the group?
Have the fourth person in each group take a protractor and measure the height of the Sun (or the string line, in this case) in degrees.
How high is our Sun in degrees above the paper? How long was the shadow? Let's record these numbers on the bottom of the paper somewhere.
Erase the first Sun and draw another significantly lower on the board and redo this entire procedure for that new height.
What does this triangle look like? How is it different from the first one? What is the height of our Sun? What is the length of the shadow?
What is happening here? There must be some relationship between the height of the Sun and the length of shadow it makes, but we knew this from our experiences outside. There also seems to be some mathematical relation between that angle of the triangle and the length of the triangle's bottom side. Did the size of the toothpick ever change? No. This makes a steady length for one side of the triangle. Maybe we could think about that some more. Is there a fraction we could think about that might change as the small angle changes? How about the toothpick length divided by the shadow length? What is the number? Is it greater than one here (for the first set of numbers, write them on the easel as a fraction.) How big was the angle? And what about for the other set?
Write them on the easel also (if there is any room left, that is!).
How big was its angle? We seem to find that the bigger the angle, the bigger the fraction. Cool. Do we have any other data we can check? Let's gather all of our data in one place so we can look for patterns, if there are any!
Start a table on a new sheet on the easel. The table should have room enough for 7 columns, with Time and Length of Shadow and Length of Stick as headers for columns 1-3. Obviously, the third column will not change!
Let's think about how we have gotten data so far. The first column we know because we were careful to write down the time each time we took a measurement. The second column we had to measure ourselves with a ruler. The third column we knew already, because we had measured the stick. What else have we been talking about that we can figure out about this system of three lines, stick, shadow, and ray of sunlight?
They should continue thinking about the idea of the triangle and that fraction.
How might we really find the angles we want to know about? Does anyone suggest using the string idea on the real setup?
Set up the stick and paper on the floor. Let students use string to connect the top of the stick to the end of the first shadow. Someone can then measure the angle made at the paper with the string and write this into a measured angle column. They should do this for all of the shadow lengths.
Look only at the sun stick drawings, not the Hello, Sun! set. How long was our stick? It was one foot, or 12 inches, or if you used a half-meter stick, it was 50 centimeters. What are the lengths of these shadows?
A group should measure the lines and record the lengths in the table (using centimeters is just as valid as using feet or inches). Can they make a fifth column for the fraction and fill it in? If not, you might consider using a calculator and giving them fractional values for the numbers they call out.
Is there a pattern? Could we make some guesses based on the sizes of the fractions as to what the angles might have been for those times?
We are so close to being able to find an angle from this information, even though we have one we think we measured correctly. If this relationship is so simple, is there a table somewhere?
Producing a table of tangents might be cool. It is not  possible to expect these students to read the table very well, nor is it reasonable to expect them to understand radians of a circle. So, it is suggested that you instead tell them the calculator has the table built in. Yes, really. And for each fraction we find, we can find the angle that goes with it. Do this for each tangent fraction and write the calculated angle in on the easel in a sixth column.
possible to expect these students to read the table very well, nor is it reasonable to expect them to understand radians of a circle. So, it is suggested that you instead tell them the calculator has the table built in. Yes, really. And for each fraction we find, we can find the angle that goes with it. Do this for each tangent fraction and write the calculated angle in on the easel in a sixth column.
The trick here is, if they have not suggested it already, is that the Hello, Sun! drawing has fists drawn in to indicate height. Since a fist is about 10 degrees, we can see how the angles match. If someone can call out the fist measurement, the rest should be able to tell you the degrees. Write fist degrees into the seventh and final column. The two last columns will not be perfectly matched, but they will be close. Ask them which measurement do they think is the less accurate and why? The fists, obviously, because the variables are the measurer's accuracy and hand size. Those who recorded the Hello, Sun! drawing should not be made fun of at this point, but should be reminded that if their eyesight was as perfect as the math, they would be in the Guinness Book of World Records! Human error is a fact of life.
How could we have made mistakes in the math? The way we typed data into the calculator, the way we measured the shadow length, or the wiggling of the sun stick outside in the first place.
What are we looking to find out from this work, anyway?
Probe the class for what ideas they might be having about why we are doing this today. Some may think about the height of the Sun changing, because they can see from the Hello, Sun! data that it is. Some may think we are trying to learn more about triangles and angles. Others may think this is a load of malarkey. OK, two out of three isn't bad. The gist is to see if we can use three different means of finding the same answer, to prove that if the logic is correct, the method is irrelevant in finding the answer. So many times we discourage children from using their own problem solving techniques because we ourselves have not internalized their method enough to comprehend if it is sound. Hopefully, after this investigation, students will see that a few minutes of thought can create three separate means of finding the same value for the Sun's angle.
Encourage your class to think about how each method was different in terms of accuracy, levels of math and observation, and simplicity.
The last thing to think about with this single data set is the time it took for the Sun to zip across the sky or the shadows to zip across the paper during the day. The pattern of shadows makes a big fan on the paper. How would you use the protractors to find out things about the pattern? Are there any places where you would want to measure angles?
Let them measure for a while. Then ask what the is biggest angle they can find. It will be the angle between the first and last shadows.
What is this angle? What does it represent about the Sun itself? How long did it take the Sun to travel that far? Subtracting the times listed on the shadows, it is (if you measured from, say, 9 a.m until 2 p.m.) five hours. So, the Sun moved so many degrees (ends up being 75) in five hours.
How many degrees is it around the Earth? It is 360 degrees, because the Earth is a ball. So how far around the Earth did the Sun appear to scoot in five hours? (Of course, it is the Earth spinning around like a top past a steady Sun.)
Give them time to puzzle with this. Some will ignore the 360 degrees and use the 5 instead, knowing a day is twenty-four hours. They can divide 24 hours by 5 hours and discover that 5 hours goes into 24 hours almost 5 times. So, the Earth almost went one-fifth of the way around on its axis past the Sun. Others will divide the degrees traveled in five hours into the degrees around the Earth and also give you a fraction of almost one fifth. Are both answers right? Of course they are.
How could we find out how many miles of Earth spun past the Sun in five hours? We'd need to know how many miles around the Earth is. Is there any way to find that out without looking it up? No, not yet. We need another measurement from Latitudes and Attitudes.
Measure again around the time of the winter solstice (about December 22), recreating the steps they did for the autumn equinox. After they have also observed and measured the spring equinox (about March 21) shadow lines, begin the discussions for the end of the coming Thread Tilt-A-World.
A note about the autumn equinox (about September 22): Since you are likely to have read this entire package ahead of time, here's a note for you. If your class has not reached this Investigation before the autumn equinox, please attempt to build and make your own record of the sun stick shadows on that day. If there are other teachers in your school who are participating in this curriculum, they could help you keep up the observations or at least watch your classroom while you run out to make these records on the equinox. You should try to measure the fist height of the Sun each time you go out, just as the kids will do. No need to measure your lines; they can do that themselves when they do the others. Curious students will want to know what you are doing, and you can tell them that soon they will be doing it as well. If it is really impossible for you to get autumn equinox data, then what is there to do? You will have two sets of data to use and not three for the next Thread.

 We
have already explored the way the Sun moves in the sky during the day. The next step is to try and see that motion from another perspective. Some classes may have been able to determine the height of the Sun in fists and found that the Sun first gets higher then lower in the sky. Did students also notice that their shadows got shorter and then longer again? Do they have a record of that? As we saw from the Thread, Me and My Shadow, the height of a light source changes the lengths and orientations of shadows. Using a standard stick with careful measurements can give us a better record of the changing shadow lengths outside in the Sun and also good data for exploring deeper.
We
have already explored the way the Sun moves in the sky during the day. The next step is to try and see that motion from another perspective. Some classes may have been able to determine the height of the Sun in fists and found that the Sun first gets higher then lower in the sky. Did students also notice that their shadows got shorter and then longer again? Do they have a record of that? As we saw from the Thread, Me and My Shadow, the height of a light source changes the lengths and orientations of shadows. Using a standard stick with careful measurements can give us a better record of the changing shadow lengths outside in the Sun and also good data for exploring deeper.
 In this Thread, we are continuing to examine the passage of time from observations we can make about the outside world. In Hello, Sun!, we saw that the Sun appears to jog across the sky during the school day. It looks like a nice and smooth motion. By using the shadow of the Sun during the day, we may make safe and accurate measurements of that motion. The National Standards require that students be learning what causes light, heat and shadow, and how time passes, how to use rulers and other measuring tools. The vocabulary words which can be introduced to help us talk about our experiences are line, length, angle, sphere, straight, and model.
In this Thread, we are continuing to examine the passage of time from observations we can make about the outside world. In Hello, Sun!, we saw that the Sun appears to jog across the sky during the school day. It looks like a nice and smooth motion. By using the shadow of the Sun during the day, we may make safe and accurate measurements of that motion. The National Standards require that students be learning what causes light, heat and shadow, and how time passes, how to use rulers and other measuring tools. The vocabulary words which can be introduced to help us talk about our experiences are line, length, angle, sphere, straight, and model.
 Download
Download

 This age group cannot yet manage the precision required for the Investigation in this Thread. They will not be able to make good measurements nor understand their importance. What we want them to learn from this adventure is that as it moves across the sky, the Sun's light changes the stick's shadow, something which they should remember from Me and My Shadow. However, we can emphasize using the Sun as a clock in this Thread. It is suggested that instead of employing the measuring stick and paper that you instead use a sapling or pole in the school yard and bright marking objects or flags. This way we can express the same basic concept in a very big and personal way, using first our bodies to mark where the shadows are and then special flags we place to make semi-permanent records of the shadows. Decorating personal flags would be a fine integration of art into this Thread for this age group.
This age group cannot yet manage the precision required for the Investigation in this Thread. They will not be able to make good measurements nor understand their importance. What we want them to learn from this adventure is that as it moves across the sky, the Sun's light changes the stick's shadow, something which they should remember from Me and My Shadow. However, we can emphasize using the Sun as a clock in this Thread. It is suggested that instead of employing the measuring stick and paper that you instead use a sapling or pole in the school yard and bright marking objects or flags. This way we can express the same basic concept in a very big and personal way, using first our bodies to mark where the shadows are and then special flags we place to make semi-permanent records of the shadows. Decorating personal flags would be a fine integration of art into this Thread for this age group.
 What is happening to the Sun outside during the day? Is it staying in one place? Does it seem to move? What happens to our shadows if the light moves? Do you think our sunlight shadows could move, too? What if we move? Do our shadows move with us? Does the Sun/Blocker/Shadow game work if we move? How could we try it out? How long would it take before we noticed any movement? Can we actually see the Sun moving? How long did it take in Hello, Sun! before we noticed the motion?
What is happening to the Sun outside during the day? Is it staying in one place? Does it seem to move? What happens to our shadows if the light moves? Do you think our sunlight shadows could move, too? What if we move? Do our shadows move with us? Does the Sun/Blocker/Shadow game work if we move? How could we try it out? How long would it take before we noticed any movement? Can we actually see the Sun moving? How long did it take in Hello, Sun! before we noticed the motion?
 Arrange ahead of time for your observation place to be undisturbed by students during the day and recess. Perhaps alerting your principal about the activity will help.
Outside, let's pick a short tree or pole (or use a standard stick) on which the school's shadow does not fall anytime during the day. It would be best if this object were near the place where we all did Hello, Sun! so similar horizon landmarks are around us. This will help us understand what is going on.
Arrange ahead of time for your observation place to be undisturbed by students during the day and recess. Perhaps alerting your principal about the activity will help.
Outside, let's pick a short tree or pole (or use a standard stick) on which the school's shadow does not fall anytime during the day. It would be best if this object were near the place where we all did Hello, Sun! so similar horizon landmarks are around us. This will help us understand what is going on.



 Back outside again in one hour ... where did the shadow move? How many things outside in our set-up could be changing? Let them decide if the stick could have changed size. Could the paper have changed size? What else is changing? Where is the Sun? (Remember not to look at directly at the Sun, as that may cause permanent damamge to the eye's retina.) Is there a connection? How long is the shadow? Where in the sky is the Sun?
Back outside again in one hour ... where did the shadow move? How many things outside in our set-up could be changing? Let them decide if the stick could have changed size. Could the paper have changed size? What else is changing? Where is the Sun? (Remember not to look at directly at the Sun, as that may cause permanent damamge to the eye's retina.) Is there a connection? How long is the shadow? Where in the sky is the Sun? 


 possible to expect these students to read the table very well, nor is it reasonable to expect them to understand radians of a circle. So, it is suggested that you instead tell them the calculator has the table built in. Yes, really. And for each fraction we find, we can find the angle that goes with it. Do this for each tangent fraction and write the calculated angle in on the easel in a sixth column.
possible to expect these students to read the table very well, nor is it reasonable to expect them to understand radians of a circle. So, it is suggested that you instead tell them the calculator has the table built in. Yes, really. And for each fraction we find, we can find the angle that goes with it. Do this for each tangent fraction and write the calculated angle in on the easel in a sixth column.
