On the unreliability of fitting
Despite some recent significant advances in Statistics and its applications to Astronomy (Cash 1976, Cash 1979, Gehrels 1984, Schmitt 1985, Isobe et al. 1986, van Dyk et al. 2001, Protassov et al. 2002, etc.), there still exist numerous problems and limitations in the standard statistical methodologies that are routinely applied to astrophysical data. For instance, the basic algorithms used in non-linear curve-fitting in spectra and images have remained unchanged since the 1960′s: the downhill simplex method of Nelder & Mead (1965) modified by Powell, and methods of steepest descent exemplified by Levenberg-Marquardt (Marquardt 1963). All non-linear curve-fitting programs currently in general use (Sherpa, XSPEC, MPFIT, PINTofALE, etc.) with the exception of Monte Carlo and MCMC methods are implementations based on these algorithms and thus share their limitations.
It has long been known that non-linear curve-fitting, for all its apparent objectivity and the statistical theoretical foundation that enables us to evaluate the goodness of fits, is still something of an art. Leaving aside issues such as a correct specification of the asymmetrical errors that are usually prevalent in astrophysical situations (mostly due to the underlying Poisson distribution), fitting a model curve to the data is never a simple and straightforward process. More often than not, the parameters returned by the programs as those that “best fit” the data are not those that truly maximize the statistical likelihood, and are caused by the programs being trapped in local minima of the chi^2 surface. Furthermore, numerical errors also creep in to the outputs based on how stopping rules are implemented: cases abound where repeated applications of the fitting program simply to move the “best-fit” parameters closer to the true best-fit values but do not ever reach it. These problems are compounded when the number of parameters in the model are large (>10), and there are significant correlations between the parameters.
A typical strategy adopted to ensure that the fitting process does result in the best possible fit, is to ensure that the fitting process begins with parameters that are very close to the true best-fit values. This is done by first carrying out the fitting in multiple stages, with only a few parameters fit at a time, holding the others fixed, until the parameter values returned by the program show that the solutions have converged. Only then is a fit to all the parameters attempted. Then, the errors on each parameter are computed by taking projections cutting through the chi^2 surface along each parameter axis, and if the best-fit values do not change during this process, then one can be confident that the best possible fit has been obtained.
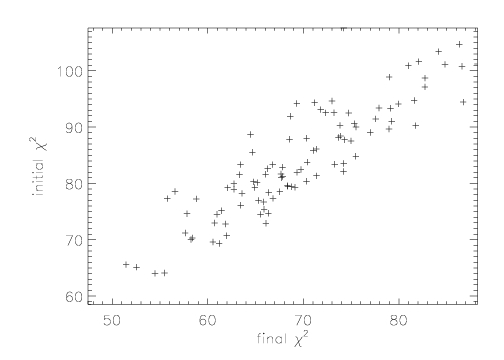
What this means in practice is that studies that carry out automated fits to a large number of data sets where there is no possibility of human intervention, and thus no means to verify that the best fit parameters have been found, are unreliable. As an example, we show in the Figure above the case where a Gaussian model was fit 100 times to profiles generated by a Poisson with a mean mu=1000 (the Poisson profile is indistinguishable from a Gaussian for mu>~100, cf. Park et al. 2006) and with a total normalization of 1000. In all cases, the fits were started with initial values at the nominal best-fit values. The Figure shows a scatter plot of the initial value of the chi^2, obtained at the end of the first fit attempt, versus the final chi^2, obtained after going through the process described above. Changes as large as delta chi^2 approx 25 are seen, which changes the character of the fit significantly.
The AstroStat Slog » All your bias are belong to us:
[...] School at Wallops Island (pdf1, pdf2), and no doubt part of the problem has to do with the (un)reliability of the fitting process when the chisq surface gets [...]
06-04-2007, 5:42 pmJeff Scargle:
… so the challenge to machine learners is to develop procedures that can at the very least flag cases as “poor fit,” and at the most respond to the situations that lead to poor fits in a robust way. Perhaps the latter would be in the form of a reported fit with large statistical and/or systematic errors reported.
07-10-2007, 2:42 pm