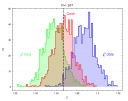
An example of chi2 bias in fitting the X-ray spectra.
The chi2 bias can affect the results of the X-ray spectral fitting and it
can be demonstrated in a simple way. The described simulations can be done
in Sherpa or XSPEC, the two software packages that allow for simulating the X-ray
spectra using a function called “fakeit”.
Here I assume an absorbed power law model with the sets of 3 parameters
(absorption column, photon index, and normalization) to simulate Chandra X-ray
spectrum given the instrument calibration files (RMF/ARF) and the Poisson noise.
The resulting simulated X-ray spectrum contains the model predicted counts with
the Poisson noise. This spectrum is then fit with the absorbed power law model to get
the best fit parameter values for NH, photon index and normalization.
I simulate 1000 spectra and fit each of them using different statistics: chi2 data variance,
chi2 model variance and Cash/C-statistics.
The next step is to plot the simulated distributions of the parameters and compare them
to the assumed values for the simulations. The figure shows the distribution of the photon
index parameter obtain from the fit of the spectra generated for the assumed simulated value
of 1.267. The chi2 bias is evident in this analysis, while the
CSTAT and Cash statistics based on the likelihood behave well. chi2 model variance
underestimates the simulated value, chi2 data variance overestimates this parameter.
vlk:
Any idea what is the primal cause of this bias? How would one understand this from a physical viewpoint? i.e., how to build intuition about it?
11-06-2007, 6:06 pmhlee:
Some sort of expansion like Taylor could characterize the bias term. Cash stat (maximum likelihood estimator) is asymptotically unbiased under mild regularity conditions but I do not think the best fit from the chi-sq function is. I guess there are ways to introduce penalized likelihoods to reduce bias (get rid of bias) designed for astronomers to get unbiased best fits. It will take time to build a connection between physical intuition and mathematical formalism, though.
11-06-2007, 9:17 pmpef:
Ah.
Tom L: if you’re reading this, you really should’ve published those notes
The short version: the optimal estimator for the photon index is the maximum
likelihood estimator. If the data are binned, and the total number of counts over
all bins is not fixed (i.e., is a random variable), then the likelihood function is
\Prod_{i=1}^k \frac{ (np_i)^{y_i} }{ y_i ! } e^{-np_i}
where y_i are the number of counts in bin i, n = \sum_i y_i, and p_i is the probability
that a count would be recorded in bin i (and this depends on the distribution
parameter, in this case the photon index).
You can derive the \chi^2 function from this using Stirling’s approximation
(np_i \gtrsim 5 in each bin) and then a Taylor series expansion. Depending on
how you do that expansion, you can derive either \chi^2 with model variance
or \chi^2 with data variance. It’s the combination of Stirling’s approximation
with how you cut off the Taylor expansion that creates the bias term.
Tom Loredo wrote this all up years and years ago, so I take no credit for the
11-07-2007, 9:59 amexplanation.
hlee:
1. The optimal estimator: Can I take that as BLUE (best linear unbiased estimator)?
11-07-2007, 12:17 pm2. Sad and glad that it’s already done. The plot and Loredo’s work should go more public.
aneta:
This is also described in Lupton book on Statistic for Astronomers in the section
11-07-2007, 9:10 pmon the ML estimators.
jk:
If you are willing to assume a likelihood, the optimal estimator is the one that maximizes the likelihood function, denoted the MLE. It is optimal in terms of efficiency ( the asymptotic variance of your estimator ). It is not, however, always going to be unbiased. However, under mild regularity conditions, the MLE is consistent, which is essentially the same as being asymptotically unbiased. If the bias is determined to be an issue, sometimes the bias can be easily corrected, take for example using s^2 to estimate sigma^2 for the case of i.i.d. normal data.
11-21-2007, 4:42 amhlee:
Details about this bias can be found from Parameter Estimation in Astronomy with Poisson-Distribution Data I. The χr2 Statistics by K.J. Mighell (1999ApJ…518..380). I overlooked references in Analysis of Energy Spectra with Low Photon Counts via Bayesian Posterior Simulation by van Dyk et al (2001ApJ…548..224). I wish that reference lists in astronomical publication include the titles so as to infer the significance of citation.
10-14-2008, 5:15 pmfillh:
It’s important to make clear this is a problem with using approximations to the true chi-square distribution for fitting Poisson-distributed data! Jading & Riisager (1996, Nuc Inst Meth Phys Res A 372, 289) do a very nice, analytical calculation of the magnitude of this effect for a particular (very simple) problem (the count-rate of a lightcurve), using both Pearson’s and Neyman’s approximations to chi-square, finding asymptotically you get a bias of around 1 count per bin.
A more general analytical discussion of the causes and magnitude of the bias for an arbitrary model is given in Humphrey, Liu & Buote (2009, ApJ 693, 822). Basically, the order of magnitude of the bias divided by the statistical error should be of order the number of bins divided by the square root of the number of photons. Fits using Pearson’s approximation to chi-square yield a bias of approximately -0.5 times the bias seen with Neyman’s approximation, and the bias on fits using the C-statistic is much smaller than the statistical error (roughly what Aneta’s plot showed).
In summary— don’t use approximations to Chi-square, but use C-statistic if you’re fitting Poisson distributed data!
09-02-2009, 8:52 pm