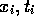 ) where
) where 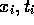 represent the magnitude and
time. of the i
represent the magnitude and
time. of the i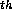 observation. Given N observations, the variance
of x is defined as:
observation. Given N observations, the variance
of x is defined as:
In the PDM method, the
period producing the least possible scatter about the derived
light curve is chosen. One does this by minimizing the sum of the
squares of the differences in the ordinate from one data point to the
next. The period resulting in the smallest sum is taken to be the true
periods. Conceptually, this has been referred to as the
``shortest string'' connecting all the data points (Dworetsky 1983).
More rigorously, any set of observations can be represented by the
ordered pair (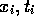 ) where
) where 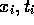 represent the magnitude and
time. of the i
represent the magnitude and
time. of the i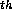 observation. Given N observations, the variance
of x is defined as:
observation. Given N observations, the variance
of x is defined as:

For this case, 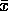 is the mean magnitude. One can calculate such a
variance for any given sample range. One is interested in minimizing
the variance of the data with respect to the mean value of the
lightcurve. To do this, one chooses a test period. Modular division
of the observation times by this test period assigns a phase to each
data point. The observations
are then grouped into bins of roughly the same phase. The variance in each
bin can now be calculated.
The overall variance is the sum of the variance of the samples:
The data are explicitly folded of each test period until the total
variance is minimized.
PDM is well suited to small and randomly spaced samples.
This method has no preference for a particular
shape (e.g., sinusoidal) for the curve.
is the mean magnitude. One can calculate such a
variance for any given sample range. One is interested in minimizing
the variance of the data with respect to the mean value of the
lightcurve. To do this, one chooses a test period. Modular division
of the observation times by this test period assigns a phase to each
data point. The observations
are then grouped into bins of roughly the same phase. The variance in each
bin can now be calculated.
The overall variance is the sum of the variance of the samples:
The data are explicitly folded of each test period until the total
variance is minimized.
PDM is well suited to small and randomly spaced samples.
This method has no preference for a particular
shape (e.g., sinusoidal) for the curve.