


Next: Conclusions
Up: Discussion
Previous: Evolutionary Effects
Once a star loses its disk, it appears to be free to spin--up.
In Chapter 1, it was demonstrated that 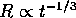 , therefore,
for a fully convective star, during a period of free spin--up,
, therefore,
for a fully convective star, during a period of free spin--up,
 . Here, t is the time that the star has
spent on the Hayashi track. This implies that the fundamental
time scale for determining the rotational period at the ZAMS
is the disk survival time,
. Here, t is the time that the star has
spent on the Hayashi track. This implies that the fundamental
time scale for determining the rotational period at the ZAMS
is the disk survival time, 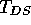 .
For example, if a 2 Myr old star is rotating at 8.25 days when loses its
disk, it will be a 4 day rotator in
6 Myr. But, if the star is 0.5 Myr old star when it loses its
disk, then, it will be a 4 day rotator in 1.5 Myr.
(Both cases assume the star is freely spinning up after disk loss.)
A star crosses the four to six day gap in the same time as
.
For example, if a 2 Myr old star is rotating at 8.25 days when loses its
disk, it will be a 4 day rotator in
6 Myr. But, if the star is 0.5 Myr old star when it loses its
disk, then, it will be a 4 day rotator in 1.5 Myr.
(Both cases assume the star is freely spinning up after disk loss.)
A star crosses the four to six day gap in the same time as  .
Choi & Herbst (1996) show that for star's rotation rate to increase
from 8 to 2.5 days, the mean of their FR distribution, is
.
Choi & Herbst (1996) show that for star's rotation rate to increase
from 8 to 2.5 days, the mean of their FR distribution, is 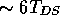 .
By the time a star reaches the
.
By the time a star reaches the 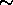 1
day periods seen in some stars in Orion OB1a and b it must have
lost their disk a relatively long time ago, and have spent only 5% of
their post--birthline, PMS lifetime with a disk.
1
day periods seen in some stars in Orion OB1a and b it must have
lost their disk a relatively long time ago, and have spent only 5% of
their post--birthline, PMS lifetime with a disk.
Many of the stars in the 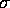 Orionis cluster have rotation periods of
about one day and are about about 2 Myr old. This means that these stars must
have lost their disk at an age of about 100,000 years, with a few losing their
disks as early as 50,000 years after
Orionis cluster have rotation periods of
about one day and are about about 2 Myr old. This means that these stars must
have lost their disk at an age of about 100,000 years, with a few losing their
disks as early as 50,000 years after 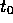 (the initial time for the
tracks.) This is quite
consistent with disk survival times measured in the Taurus--Auriga T
association (cf. Walter et al. 1988; Skrutskie et al. 1989; Wolk & Walter
1996) using both IR and spectral methods of disk detection.
(the initial time for the
tracks.) This is quite
consistent with disk survival times measured in the Taurus--Auriga T
association (cf. Walter et al. 1988; Skrutskie et al. 1989; Wolk & Walter
1996) using both IR and spectral methods of disk detection.
Stars in the Orion OB1a sample do not show a markedly different
distribution among the fast rotators. These stars are roughly 10 Myr old.
Applying the same arguments to these stars as were applied to stars near
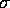 Orionis, we arrive at the conclusion that the rapid rotators here lost
their disks in at most 500,000 years. The most rapid rotation period among the
Orion OB1a stars is about 0.7 days,
which means that such a star would have lost
its disk at an age of no older than 250,000 years. This is a factor of five
higher than the similar number for the younger Orion OB1b
stars. Another way to state this result is that stars which rotate
with the same period as stars which are five times older must have held on
to their disks five times longer. But this is a just
a manifestation of the increased age of the cluster.
It is surprising that
the FR distributions look as similar as they do. If stars continue free
spin--up for the duration of their convective tracks, (all but five
X--ray active stars in the Orion OB1a sample are still on their
convective tracks) then the Orion OB1a
stars should show much faster periods
than the Orion OB1b sample. This is not the case. Assuming this
model is correct, it is hard to understand why
the physical conditions of these stars would be different
in exactly the right way so that the rotation period distribution of
the slow rotators looks the same in two associations of different age.
The point is,
the simple free spin--up after disk loss model does not quite work
and the other mechanisms must come into play.
Orionis, we arrive at the conclusion that the rapid rotators here lost
their disks in at most 500,000 years. The most rapid rotation period among the
Orion OB1a stars is about 0.7 days,
which means that such a star would have lost
its disk at an age of no older than 250,000 years. This is a factor of five
higher than the similar number for the younger Orion OB1b
stars. Another way to state this result is that stars which rotate
with the same period as stars which are five times older must have held on
to their disks five times longer. But this is a just
a manifestation of the increased age of the cluster.
It is surprising that
the FR distributions look as similar as they do. If stars continue free
spin--up for the duration of their convective tracks, (all but five
X--ray active stars in the Orion OB1a sample are still on their
convective tracks) then the Orion OB1a
stars should show much faster periods
than the Orion OB1b sample. This is not the case. Assuming this
model is correct, it is hard to understand why
the physical conditions of these stars would be different
in exactly the right way so that the rotation period distribution of
the slow rotators looks the same in two associations of different age.
The point is,
the simple free spin--up after disk loss model does not quite work
and the other mechanisms must come into play.
Observational biases should not account for this discrepancy
since both the Orion OB1a and OB1b
samples were subject to the same criteria. Nor is there evidence for an
intrinsic difference between the star formation mechanisms in Orion OB1a and
those in Orion OB1b and the Taurus T association. Instead, these data are
suggestive of
an internal braking mechanism which prevents stars at certain evolutionary
epochs from exceeding a certain spin rate. It is unclear as of yet how such
braking mechanism would work, but it should be pointed out that stars of
greater than
0.5 M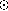 develop radiative cores while still on their convective tracks
(Barnes 1996). It is possible for internal braking to occur
between the convective and radiative zones of stars still on their putative
convective tracks. Barnes & Sofia (1996) argue for a saturation of
angular momentum loss beyond a threshold speed. If the magnetic
field is proportional to some power of the rotational period
(
develop radiative cores while still on their convective tracks
(Barnes 1996). It is possible for internal braking to occur
between the convective and radiative zones of stars still on their putative
convective tracks. Barnes & Sofia (1996) argue for a saturation of
angular momentum loss beyond a threshold speed. If the magnetic
field is proportional to some power of the rotational period
(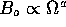 , Linsky et al. 1983),
and the magnetic field is subject to saturation, this will
naturally slow the acceleration of the rotational period.
The models of Barnes & Sofia were designed to explain UFRs to
which the data presented here are not sensitive.
However, their results show that angular momentum saturation does brake
stars at an age of 70 Myr. In their model,
such braking commences at an age of 2 Myr and has a significant effect by the
age of 10 Myr. Therefore angular momentum saturation could be the
cause of the similarity among the distributions of the fast rotators.
, Linsky et al. 1983),
and the magnetic field is subject to saturation, this will
naturally slow the acceleration of the rotational period.
The models of Barnes & Sofia were designed to explain UFRs to
which the data presented here are not sensitive.
However, their results show that angular momentum saturation does brake
stars at an age of 70 Myr. In their model,
such braking commences at an age of 2 Myr and has a significant effect by the
age of 10 Myr. Therefore angular momentum saturation could be the
cause of the similarity among the distributions of the fast rotators.



Next: Conclusions
Up: Discussion
Previous: Evolutionary Effects
Scott J. Wolk
Thu Dec 5 15:48:37 EST 1996
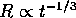 , therefore,
for a fully convective star, during a period of free spin--up,
, therefore,
for a fully convective star, during a period of free spin--up,
 . Here, t is the time that the star has
spent on the Hayashi track. This implies that the fundamental
time scale for determining the rotational period at the ZAMS
is the disk survival time,
. Here, t is the time that the star has
spent on the Hayashi track. This implies that the fundamental
time scale for determining the rotational period at the ZAMS
is the disk survival time, 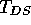 .
For example, if a 2 Myr old star is rotating at 8.25 days when loses its
disk, it will be a 4 day rotator in
6 Myr. But, if the star is 0.5 Myr old star when it loses its
disk, then, it will be a 4 day rotator in 1.5 Myr.
(Both cases assume the star is freely spinning up after disk loss.)
A star crosses the four to six day gap in the same time as
.
For example, if a 2 Myr old star is rotating at 8.25 days when loses its
disk, it will be a 4 day rotator in
6 Myr. But, if the star is 0.5 Myr old star when it loses its
disk, then, it will be a 4 day rotator in 1.5 Myr.
(Both cases assume the star is freely spinning up after disk loss.)
A star crosses the four to six day gap in the same time as  .
Choi & Herbst (1996) show that for star's rotation rate to increase
from 8 to 2.5 days, the mean of their FR distribution, is
.
Choi & Herbst (1996) show that for star's rotation rate to increase
from 8 to 2.5 days, the mean of their FR distribution, is 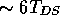 .
By the time a star reaches the
.
By the time a star reaches the 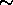 1
day periods seen in some stars in Orion OB1a and b it must have
lost their disk a relatively long time ago, and have spent only 5% of
their post--birthline, PMS lifetime with a disk.
1
day periods seen in some stars in Orion OB1a and b it must have
lost their disk a relatively long time ago, and have spent only 5% of
their post--birthline, PMS lifetime with a disk.
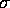 Orionis cluster have rotation periods of
about one day and are about about 2 Myr old. This means that these stars must
have lost their disk at an age of about 100,000 years, with a few losing their
disks as early as 50,000 years after
Orionis cluster have rotation periods of
about one day and are about about 2 Myr old. This means that these stars must
have lost their disk at an age of about 100,000 years, with a few losing their
disks as early as 50,000 years after 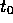 (the initial time for the
tracks.) This is quite
consistent with disk survival times measured in the Taurus--Auriga T
association (cf. Walter et al. 1988; Skrutskie et al. 1989; Wolk & Walter
1996) using both IR and spectral methods of disk detection.
(the initial time for the
tracks.) This is quite
consistent with disk survival times measured in the Taurus--Auriga T
association (cf. Walter et al. 1988; Skrutskie et al. 1989; Wolk & Walter
1996) using both IR and spectral methods of disk detection.
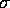 Orionis, we arrive at the conclusion that the rapid rotators here lost
their disks in at most 500,000 years. The most rapid rotation period among the
Orion OB1a stars is about 0.7 days,
which means that such a star would have lost
its disk at an age of no older than 250,000 years. This is a factor of five
higher than the similar number for the younger Orion OB1b
stars. Another way to state this result is that stars which rotate
with the same period as stars which are five times older must have held on
to their disks five times longer. But this is a just
a manifestation of the increased age of the cluster.
It is surprising that
the FR distributions look as similar as they do. If stars continue free
spin--up for the duration of their convective tracks, (all but five
X--ray active stars in the Orion OB1a sample are still on their
convective tracks) then the Orion OB1a
stars should show much faster periods
than the Orion OB1b sample. This is not the case. Assuming this
model is correct, it is hard to understand why
the physical conditions of these stars would be different
in exactly the right way so that the rotation period distribution of
the slow rotators looks the same in two associations of different age.
The point is,
the simple free spin--up after disk loss model does not quite work
and the other mechanisms must come into play.
Orionis, we arrive at the conclusion that the rapid rotators here lost
their disks in at most 500,000 years. The most rapid rotation period among the
Orion OB1a stars is about 0.7 days,
which means that such a star would have lost
its disk at an age of no older than 250,000 years. This is a factor of five
higher than the similar number for the younger Orion OB1b
stars. Another way to state this result is that stars which rotate
with the same period as stars which are five times older must have held on
to their disks five times longer. But this is a just
a manifestation of the increased age of the cluster.
It is surprising that
the FR distributions look as similar as they do. If stars continue free
spin--up for the duration of their convective tracks, (all but five
X--ray active stars in the Orion OB1a sample are still on their
convective tracks) then the Orion OB1a
stars should show much faster periods
than the Orion OB1b sample. This is not the case. Assuming this
model is correct, it is hard to understand why
the physical conditions of these stars would be different
in exactly the right way so that the rotation period distribution of
the slow rotators looks the same in two associations of different age.
The point is,
the simple free spin--up after disk loss model does not quite work
and the other mechanisms must come into play.
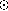 develop radiative cores while still on their convective tracks
(Barnes 1996). It is possible for internal braking to occur
between the convective and radiative zones of stars still on their putative
convective tracks. Barnes & Sofia (1996) argue for a saturation of
angular momentum loss beyond a threshold speed. If the magnetic
field is proportional to some power of the rotational period
(
develop radiative cores while still on their convective tracks
(Barnes 1996). It is possible for internal braking to occur
between the convective and radiative zones of stars still on their putative
convective tracks. Barnes & Sofia (1996) argue for a saturation of
angular momentum loss beyond a threshold speed. If the magnetic
field is proportional to some power of the rotational period
(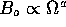 , Linsky et al. 1983),
and the magnetic field is subject to saturation, this will
naturally slow the acceleration of the rotational period.
The models of Barnes & Sofia were designed to explain UFRs to
which the data presented here are not sensitive.
However, their results show that angular momentum saturation does brake
stars at an age of 70 Myr. In their model,
such braking commences at an age of 2 Myr and has a significant effect by the
age of 10 Myr. Therefore angular momentum saturation could be the
cause of the similarity among the distributions of the fast rotators.
, Linsky et al. 1983),
and the magnetic field is subject to saturation, this will
naturally slow the acceleration of the rotational period.
The models of Barnes & Sofia were designed to explain UFRs to
which the data presented here are not sensitive.
However, their results show that angular momentum saturation does brake
stars at an age of 70 Myr. In their model,
such braking commences at an age of 2 Myr and has a significant effect by the
age of 10 Myr. Therefore angular momentum saturation could be the
cause of the similarity among the distributions of the fast rotators.