

Practicality aside, being able to read and understand a map is an important analytical skill. Mapping has been a part of our lives since the very first explorers set forth to chart the lands beyond their countries. After centuries of such adventures, very little of the Earth's surface is yet uncharted. Orbiting satellites also have been making many detailed maps of the Earth's surface. However, much of the most exciting mapping being done today happens from our explorations away from the Earth! Several robotic space missions have traveled to other planets to map their surfaces. Most recently, the Magellan space probe which orbited Venus made a detailed radar map of its terrain, obscured by Venus' thick atmosphere. The CfA Redshift Survey is a project of over a decade which is mapping the galaxies of the entire Universe!
Whether a map is of a classroom, a city, a planet, or an Universe, the same basic knowledge is required to understand the information it contains: scale, orientation, angles, and measurement. In this chapter, we practice reading maps, first of our nearby surroundings, then of our town, and then of the Earth and stars. We begin this topic by using maps, then learning how to make our own.
Whether to get across town or across the world, maps are crucial for navigation. They can help us discover the distances between objects and their relative orientation to one another.
The ideas of following direction and relating to a two-dimensional representation of a landscape are to be introduced first with a fun scavenger hunt. The chapter will then move on to political maps, and then see how topographical maps describe terrain.
Activity 4-1: Scavenger Hunt
Scavenger hunts are always fun, but in this hunt, the rewards include not just the "goodies" found on the course, but also the skill of following a map.
Materials: An interesting, yet safe and supervised, course for the hunt; a simple, handmade map of the course; small prizes like toys, trading cards, booklets of stories, etc.
Discussion
Were the students able to find all of the goodies? Could they find all of the reference points? Which ones were easier to find? Were they able to find topographical features like hills. Would compass directions help? What about distant landmarks? What makes a good map? What should a map convey? Are all maps meant for the same purpose? How might the map had been different if the students were driving cars or flying planes instead of walking around?
Activity 4-2: Follow a Map of the Town
Instead of looking at a map of a small area, like the playground, we will look at a larger area: our home town or city. See how many landmarks the students can find. Can they find where they live? Can they find their school? You should make a list of places for each student or group to find. The type of places which can be found depends greatly on the type of map available.
Materials: Road map of city or town; list of places, landmarks, or streets to find; rulers.
Discussion
If one map has a scale of "1 inch = 1 mile" and another has "1 inch = 10 miles", which map covers more area? Which map can show more detail? Is a map with more detail always better? What kind of information might a political map have which a topographic map might not? What kind of information would a nautical chart have? Can anyone think of a problem with making a map of the entire Earth? Hint: is the Earth flat like the map?
Activity 4-3: Topographic Maps
In 1960, the federal government conducted a complete topographical survey of the United States. The commission responsible for this survey, the United States Geological Survey Commission, has field-checked and updated the Survey several times in the years since. The Survey maps show features of the land, like lakes, ponds, rivers, and streams, and man-made landmarks like permanent buildings, roads, churches, graveyards. They are very detailed, being of the scale 1:24,000; one centimeter on the map represents 24,000 centimeters (240 m or 0.24 km) on the Earth (in English units, one inch represents about 0.38 miles). Neither the roads nor the buildings are labeled, however; these maps are intended to record surface features, especially variations of altitude. To do this, there are contours drawn on the maps, to indicate 10-foot variations in altitude. As a result, these maps are able to convey a sense of the three-dimensional lay of the land. In this activity, we will compare the Survey maps with the land they represent.
Materials: Topographic map available from the U.S. Geologic Survey (details below).
Discussion
Who might use a map like this? Is it a good road map? Does it should political boundaries like precincts, counties, and states? What sorts of uses would this map have that, say, a sightseeing map wouldn't? Why bother recording altitude? Can you think of way other than contours to record it? If the contours on a hill are closer together, does that mean the hill is more or less steep than one whose contours are farther apart?
Now that the students have had some experience using and interpreting maps, the next logical step is to try to make some. We'll start small- literally - by mapping a small, familiar area, the classroom. We'll then venture outside and map the school grounds.
Activity 4-4: Making and Using a Trundle Wheel
It is suspected that in the making of the precise dimensions of the Egyptian Pyramids, architects used a device known as the trundle wheel. We have often used rulers or meter sticks to measure distances, but this requires several steps: placing the ruler down, marking the far end of the ruler, lifting the ruler up and putting the close end on the mark, marking the far end, etc., until the distance is measured. Even using a flimsy tape measure requires several people to hold one end firm, to keep the tape from flipping, to measure the end, etc. The trundle wheel, however, relies on the simple fact that a circle with a known circumference can be used as a ruler. The circumference is the distance around any circle. Take a string one foot long and bring the ends together to form a circle -- the circumference of this circle is one foot. Rolling a circle with a known circumference along on its edge and counting how many times the circle can go around will tell you how many feet make up that distance you rolled it.
Materials: Big pieces of cardboard (a movers box is fine), scissors or blade, meter stick with hole at end or strong, narrow piece of cardboard resembling such, brass fasteners, dark marker, ruler and a drawing compass
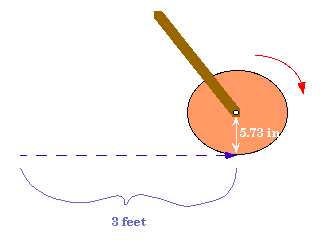 These trundle wheel sizes are convenient for measuring distances as big as rooms or as small as the distances between desks. For the 1 ft trundle wheel, spread the two legs of the compass such that one end points to the zero line on the ruler and the other lines up with a little less than 2 inches (the radius). Lock the compass if you can, otherwise, be careful not to accidentally readjust them. Firmly stick the pin end of the compass into the cardboard and swing the pencil end around on the cardboard outlining a circle.
These trundle wheel sizes are convenient for measuring distances as big as rooms or as small as the distances between desks. For the 1 ft trundle wheel, spread the two legs of the compass such that one end points to the zero line on the ruler and the other lines up with a little less than 2 inches (the radius). Lock the compass if you can, otherwise, be careful not to accidentally readjust them. Firmly stick the pin end of the compass into the cardboard and swing the pencil end around on the cardboard outlining a circle.
Discussion
Are the trundle wheels easier to use than the meter sticks? Are the measurements different? Can students make their own wheels of different sizes using the circumference relationship to the radius? What are the advantages and disadvantages of the trundle wheel? Can students think of other shapes which might be good measuring tools?
Activity 4-5: Mapping the Classroom
For our first mapping exercise, we'll start small- literally- by mapping the classroom. First we'll examine the room, and discuss the objects in it. Then we'll build a scale model on a large sheet of paper. By tracing the objects we've placed on the paper to represent things in the room, we will have created our first map. The students can then develop a key to represent all of the objects in the room, and then they can make their own versions using their key.
Materials: Trundle wheels or tape measures; small wood scraps (enough of uniform size and approximate scale to represent desks, etc.); large chart paper (cut from 3-4 foot roll); rulers; pencils; markers; 9"x 18" white construction or oaktag paper; stencils of small shapes.
Discussion
What reference points were the most helpful when starting to map the classroom? Why? How does a key simplify making the map? Would it be more or less work to try to capture the distinct shape of each and every piece of furniture? When might it be necessary to record each shape? How does scale help one make sense of a map? Classes from different rooms could team up, exchange maps, and try to find their partners' desks. Visiting parents could try to use the maps to find their children's desks.
Activity 4-6: Perspective and Reference Points
As students begin to make maps, the importance of scale and perspective become clear.
Materials: Teddy Bear or any suitable objects; large picture; variety of different size balls; paper; markers; blocks; construction paper, 18"x 24".
Discussion
How does measuring with tools help us to make a map? Does it make any difference where you stand when you make a map? Do objects look smaller from one place than from another? How does this effect your map? How can this help students in their map making? If students make another map of their playground (Activity 4 of this topic) will they do it differently? How can they use the measuring reference points in making maps? Would it change the way you made a map if you stand in another place to make it? How can you devise a system to represent the area and the objects in it so that they will be the same relative size or scale on your maps?
Activity 4-7: Mapping the School Grounds
The move outside provides students with different mapping challenges; scale, elevation, and topology take on added importance. Students learn by developing their own techniques for showing these; only when they have experienced this, they will benefit from materials for measurement of elevation such as large rods and levels. Through representations they will increasingly see the relationships between the three-dimensional world and the two-dimensional symbols which represent it on their maps.
When mapping a large area outside, such as the school yard, what tools will help you to make a map? Can you show how far away objects are after you measure them? Does it matter if you move around or should you stand in the same place? How can you use the compass to help you place objects? How can you represent directions accurately? How could you show the hilly parts of the land.
Materials: Large sheets of paper (one for each group of two students), with outline of school grounds and a few key features; pencils; measuring devices; yardsticks; trundle wheels, string; directional compasses.
Discussion
Students discuss their results. Were their maps similar? What problems did they encounter? How did they represent changes in elevation? What about various surfaces? How did they established directions? What kind of symbols did they use?
Activity 4-8: Mapping the City or Town
The step to mapping a larger area is the next in our investigation of mapping. Representing one's school and playground on a large map allows students to trace their routes to school by moving model cars and buses on the map. The streets represented may lead to major buildings such as libraries, fire and police stations, and town and city halls. Directionality may be established and a compass rose included in the map. Students may work from a map of their town which has been enlarged and then enlarge that again. Students may map a route to a playground or other area of interest and then walk that route together.
How could students help to map an area when the whole area cannot be seen? What materials would be helpful to use in making such a map? What unit of measure would be appropriate to use? If the school is the focus point and placed at the center of the map, how could students represent it? What other buildings would they want to represent on this map? What about other areas of their town? How could they make a very large map even large enough to walk on? How could they determine directions?
Materials: One large sheet (3'x 8') of heavy paper from standard 3' roll for each group; wide tape; yardstick; pencils; markers; photographs of buildings; large piece of heavy plastic to cover map; blocks of wood; map of students' town or city (enlarged to largest size possible on large capacity copy machines); plastic figures and cars; oaktag; glue.
Discussion
Was this activity helpful to the students? In what ways? If they had to map an area foreign to them, how might they start? How would they measure large distances? Can the students find their own streets? If so, can they locate where their houses should be? If students were building a new town or city, how would they plan it? What would they include? exclude? What would they do differently?
A coordinate system is just a way of systematically denoting and labeling points in space. Numbered aisles in supermarkets, grids on road maps, and lines of latitude and longitude on the Earth are all coordinate systems which we use every day. Coordinate systems are usually based on two lines, or axes, which are most often perpendicular to one another. In a city, for instance, one building may be "two blocks north and four blocks east", from another, in which case the compass directions of north and east are used as a basis for the grid of the city.
Activity 4-9: Reference Directions on the Earth
On the Earth, we use the directions of the compass for reference: Boston is north and east of New York, San Diego is south of Los Angeles. Canada is north of the United States and Mexico is south. The direction "north" is defined as the direction from any point on the globe towards the North Pole, where the axis of rotation of the Earth sticks out of the surface in the Northern Hemisphere. Similarly, "south" is towards the South Pole. We usually look at maps and globes where North is on the top. Why might this be? Are the two hemisphere's equally populated? Do you think " north is up" seems natural to people in Australia?
If one faces north and extends ones arms straight out to the sides, the left hand points to the west and the right to the east. Looking at a compass rose, one can remember this because the "W" of west and the "E" of east spell a word - "WE" - if they are properly aligned - "EW" is not a word! The Earth is spinning about its axis such that its surface moves eastward. This is why the Sun and Moon and the stars all rise on the eastern horizon, move westwardly through the sky, and set on the western horizon.
In this activity, we use the midday shadow to find true north, much as in the activity "Sun Shadows" of Chapter 1. If there is not sufficient time (or suitable weather) to use the shadow stick, a compass may be used instead, but keep in mind that the compass points towards magnetic north, not towards the North Pole of the Earth.
Materials: Shadow stick from activity "Sun Shadows" of Chapter 1; large piece of paper; markers; rock or brick.
Discussion
Is north always the same direction for everyone? What are the advantages of using such a "global" coordinate system? Are there any disadvantages Why not just use directions like "three blocks to the left" or "a mile and a half to the right"? Do these directions make assumptions about the traveler's original position and orientation? Are these directions better for local areas or larger areas? If northeast (NE) is halfway between north and east, where might north by northeast (NNE) be? Where would south by southwest SSW be? If something is northeast of you, what direction are you from it?
Activity 4-10: Mapping on a Grid
This activity will introduce the students to mapping on a grid. While most grids we map by are made of invisible, imaginary lines, the lines of our grid in this activity are clearly visible, the cracks between linoleum floor tiles. Having placed objects on such a grid, the students can then try mapping the area on some graph paper, essentially a scaled down version of the grid. Once the concept of a map on a grid is understood, specific grids like latitude and longitude should make more sense to the students. A great game to play with the students to give them practice with grids is the game of Battleship.
Materials: Linoleum tile floor; masking tape; Post-it pads; markers; objects like blocks, balls, books, boxes to place on the grid; sheet of graph paper for each student.
Discussion
Did the grid help to map the area? How? What kind of maps use grids? Do grids help on interstate highways maps? Why or why not? Are there any grids on the Earth with lines we can see like the ones on the floor?
Activity 4-11: Latitude and Longitude on the Earth
The dawn of the Great Age of Discovery, some five hundred years ago, greatly increased the demand for accurate maps and charts. The explorers needed maps which covered areas much more vast than those we have yet constructed; they required maps of nothing less than the entire world which they were exploring. 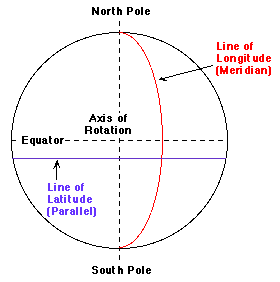 Indeed, much of the work of these early explorers involved making newer, more accurate maps of little- or never-traveled regions.
Indeed, much of the work of these early explorers involved making newer, more accurate maps of little- or never-traveled regions.
Even still, it was not until about a century ago that a standard coordinate system to describe locations on the Earth's surface was adopted. An international convention devised the now-familiar system of latitude and longitude and fixed its reference points. As illustrated in the figure, a line of longitude (a meridian) passes through both the North and South Poles. They are labeled according to their angular distance from the prime meridian which passes through Greenwich, England by international agreement. Meridians are labeled between 0° and 180° East or West of the prime meridian. Lines of latitude (often called "parallels") are parallel to the Equator, and are labeled according to angular distance from the Equator- between 0° and 90° North or South. Any point on the surface of the Earth can be uniquely specified by just these two coordinates, latitude and longitude.
Materials: Globe or map of world and local maps with clearly marked latitude and longitude scales; list of cities (on world map) or landmarks (on local map) to find by latitude and longitude coordinates.
Discussion
The lines of latitude and longitude are not straight, since they are on the surface of a sphere. Nevertheless, if one looks at a small enough region, like a city or a town, that region of the Earth is nearly flat, so the lines of longitude and latitude appear straight and seem to form a square grid. Note that close to the Poles, where the meridians converge, the slant of the meridians is quite noticeable, even on small scales, so even if they appear straight, they won't form a square grid.
It is possible to determine your latitude and longitude from observations of the night sky wallpaper. Finding your latitude in the northern hemisphere is the easiest, as it only requires one night's observation of the Pole star. This figure shows a diagram of the Earth with the dashed lines denoting the Earth's equator and the axis of spin. We've placed a small figure of a person on the Earth to show someone observing from a city on the Earth. 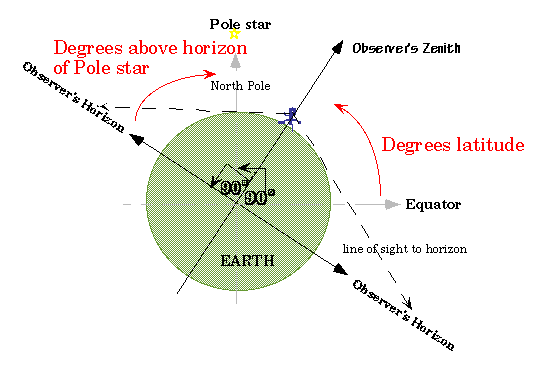
Notice that tracing the line straight up to the zenith point for this observer makes an angle with the equator which is the degrees latitude for this observer (since latitude is defined as the angle above or below the equator). Also notice that the horizon for this observer is marked as the diameter of the Earth perpendicular to the zenith line, or 90° below the zenith point in all directions, defined as such because you can look straight out as well as straight up. Thus, the equator of the earth, if extended up to the sky, is not on the horizon of this observer, but is above it by a number of degrees which are difficult to determine! So, how do we find out how many degrees from the equator, i.e.; degrees latitude, our city is? The figure below shows you that since you know the equator is 90° from the pole by definition and our latitude is 90° from our horizon by definition, that 90° minus our degrees latitude equals 90° minus the height (in degrees) of the Pole star over the horizon OR our degrees latitude equal the degrees of height of the pole star over the horizon! Using the fists method, students can count how many fists and fingers above the horizon they see the Pole Star and that is how many degrees above the equator they are!
Activity 4-12: Calibrating your fist
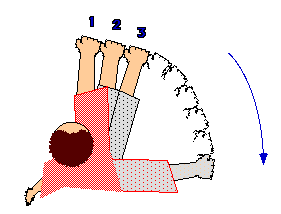 All you need to know is that 90° is the angle between holding your arm straight out to the side and straight out in front of you. All you need to do is stand still and put your arm out in front of you at eye level, with your hand in a fist. Close one eye. Carefully begin moving your arm stiffly, watching and counting how many fists you can line up side by side until your arm is 90° away from where you started, or straight out to your side. Use things around the yard as guides to help you count those imaginary fists. The figure helps you see what we are describing. Dividing 90° by the number of fists you counted will give you how many degrees your fist covers! (Hint: In case you are not sure of your answer, an average fist covers 10° on the sky. Your value should be close to this.) Similarly, you can try to calibrate your finger! But we will tell you that the human finger held at arm's length will cover 1° on the sky.
All you need to know is that 90° is the angle between holding your arm straight out to the side and straight out in front of you. All you need to do is stand still and put your arm out in front of you at eye level, with your hand in a fist. Close one eye. Carefully begin moving your arm stiffly, watching and counting how many fists you can line up side by side until your arm is 90° away from where you started, or straight out to your side. Use things around the yard as guides to help you count those imaginary fists. The figure helps you see what we are describing. Dividing 90° by the number of fists you counted will give you how many degrees your fist covers! (Hint: In case you are not sure of your answer, an average fist covers 10° on the sky. Your value should be close to this.) Similarly, you can try to calibrate your finger! But we will tell you that the human finger held at arm's length will cover 1° on the sky.
Activity 4-13: Measuring your latitude
Materials: Paper and pencil.
Discussion
What kinds of values did the students get for their latitude? Checking with the real latitude of your town, how accurate were these measurements? Could the students find this fists method useful for measuring other heights? Distances between stars on the sky? Sizes of constellations? Diameter of the moon (1/2 °, or a pencil held at arm's length!)? Perhaps further night observations will allow students to make star atlases describing the constellations in terms of degree sizes on the sky.
Activity 4-14: Mapping the Sky
The visible stars can be used as markers on the sky which can be placed on a map. Such star maps are useful not only to astronomers trying to find a certain star with a telescope but also to children trying to find the Big Dipper. Making a map of the entire sky is similar to making a map of the entire world - both are round and too big to observe all at once, for example. It turns out that celestial maps use a coordinate system very similar to latitude and longitude of their terrestrial counterparts, but on a sky map these coordinates are called "right ascension" and "declination".
These activities can be used either to help students become familiar with constellations before locating them or to help reinforce their observations and help them learn. It may be useful to use these activities to introduce the concept of magnitude of stars. Magnitude is the term used to define the brightness of a particular star. The brighter the star, the lower the magnitude number. The brightest stars have magnitudes from negative numbers up to around 3. The brightest star we can see is Sirius in the constellation Canis Major, which is visible in January and February. It has a magnitude of -1.42. This star is labeled on the Star Map included in Activity 1 of this topic. Conversely, the fainter stars have higher magnitudes. A star whose magnitude is 6 is difficult to see without an optical aid. Also, stars differ in color. They range from the hottest which are blue, then green, white, yellow, orange and red, in descending temperature. Stars appear to twinkle although giving off steady light as our sun does because of the atmosphere of the Earth. Therefore , stars just above the horizon appear to twinkle more than stars up above us because we are viewing them through more density of the Earth's atmosphere at the horizon.
Discuss constellations and stars already found. What questions do students have? What would they name these patterns or individual stars if they were just discovering them and making order out of them? They may share their ideas about new shapes and configurations from existing star patterns. Some students may want to make up stories to give more meaning to their ideas or this could be a group activity. One person might begin to tell a story about his new creation/constellation and others add to it around a circle. Did the ancients tell stories this way? Without writing down the story, tell it again the next day or week. Does it change? What value would be gained from writing these stories down? What value might be lost?
Activity 4-15: Introduction to Mythology and Storywriting
This may be an appropriate time to introduce the study of Greek mythology since many of the constellations were named by ancient Greeks. After students have found many constellations the stories will capture their attention and have more meaning for them. Students may do research to find out about the Greek gods and goddesses such as Zeus, Athena, Hera, Apollo, Hermes and others. They may enjoy hearing myths as well as reading them. Perhaps they would enjoy hearing a story for each of the zodiac constellations. These are told in a beautifully illustrated book, The Shining Stars: Greek Legends of the Zodiac.. A companion book to this is The Way of the Stars: Greek Legends of the Constellations or Dauliere's Greek Myths (for older students). These are listed in the bibliography. Myths often were told because there was a problem that needed to be solved and it was solved within the myth. Students may write their own myths, creating their own gods, goddesses, and part god, part human characters. They too will work through their problems as they learn to write and develop their creativity. Myths often explained natural phenomena. This activity may be enlarged to hearing and discussing the elements of myths from different cultures. The comparisons show universality of themes across time and space. Students will find meaning by reading, listening, and writing these stories without extrapolating a moral or reason.
What is a myth? How does it differ from other stories? Why are there so many stories linking gods, goddesses and part god part human figures? What could ancient people have needed to tell, accomplish by telling stories about the constellations in the sky? If you don't know a story about a constellation could you make one up that has meaning?
Materials: Greek Myths and other myths from a variety of cultures
Activity 4-16: Understanding Star Maps
Materials: Five foot circle of heavy white paper; yarn; pencil; enlarged map of constellations for current month (available in Sky & Telescope, for instance); yardstick; silver, red, yellow, blue shiny paper; blue tempera paint (small amount of black added), watered down; crayons; colored chalk; white glue.
Discussion
How did this compare to making an earth map? Did this help students to remember the star groupings and other stars? Could they locate the constellations? North Star? What other ways could they help others to learn what they have learned? How have people used stars for maps? In what other way could this new knowledge help them in their lives? Students may choose a constellation formation, draw it and make a new form out of it. What name would they give to it? Students may discuss their observations and share theories about stars, their magnitudes, sizes, and configurations.
Activity 4-17: Understanding Distance in Space
The function of this activity is to give the students an understanding that constellations are not flat pictures in the sky, but rather the product of three-dimensional space. The stars are so far away that they appear flat, as if forming a dome above the Earth. Constellations are patterns of stars. For the most part, they are named after characters or animals in mythology. They usually do not look like what they are named for. For instance, Pegasus doesn't resemble a winged horse at all and Cygnus the swan looks more like a cross. Some, such as Canis Major (the large dog), are easier to imagine. The question of whether the stars that make up a constellation are as close to each other as they appear in the sky is a puzzle for students to solve. They should ask themselves what would they see if one star was both next to and far back from another. They should also be wondering why the sky seems flat. The following activity will demonstrate how constellations really are positioned in space, and should give students a better definition of a constellation.
Materials: Large flat field; paper plates.
What is a constellation? Are the stars in the sky all the same distance from the Earth? Why do the stars appear to be flat in the sky? What else could be in space besides stars? What do these other objects do in space? Do objects in space move? Are there patterns to the arrangement of the stars? to their movement?
Activity 4-18: Using Star Maps
Your students should be able to find the Big Dipper, North Star, and the Little Dipper from the exercises in Chapter 1. Now they will observe more constellations in the night sky.
Materials: Star charts (one for each two month period, included here); flashlight, red cellophane paper to cover lens; rubber bands; binoculars (optional); journals
Discussion
Discuss the observations as a group. Students may have been recording their activities in journals and this should help them to share more easily and accurately. Have the students share their records of the changing positions of the circumpolar stars (or dippers).
How can this pattern be useful to us? What do they notice about the other constellations over a period of time? What do they think is happening? Can they predict what the sky will look like a year from now? Why are some stars brighter than others? Different colors? Throughout this activity students may discuss, compare and predict results of these recordings. How helpful are these predictions to them in their understanding of the patterns of movement they observe in the stars? Are they able to predict the movement of the stars in the next months? Are they able to compare these observations with those form the seasons and the calendar? How can the pattern of the stars and planets help us keep records?
Activity 4-19: Making a Star Plotter
Sky mapping is an active way to make an original guide to the sky. Since students are actively engaged in this project, it will help them to view and report findings accurately. A star plotter will help them to chart the positions of the stars just as they see them in the sky. This activity provides a means of illustrating changes in the stars' positions. In this activity, students take records of where the stars have been and when they were there. This activity adds to their education of how the universe moves in orderly patterns.
Students may discuss stargazing experiences. How can they record their experiences and select what they want to remember? How could they use this information? How could they plot the stars and planets to help them learn and remember more about patterns? To explain observations to others?
Materials: Plexiglas or Lucite square about 12" by 12" (1/8-1/4" thick), strip of wood (about 6" by 1" by 1/2" thick) for handle; grease pens; tracing paper; glue for Lucite/wood or screws; drill (1/4" bit)
Activity 4-20: The Astrolabe
 When students build and use the star plotter in Activity 2, they learn to estimate angles and distances in the sky using their fists. These measurements are not very accurate. To obtain more accurate figures, an instrument may be made to help determine measurements. This is an astrolabe which was invented by the Greeks and disseminated by Islam. This instrument was used to observe and calculate the position of celestial bodies before the invention of the sextant. This activity includes two models, one simple and the other more complicated to measure angles by the stars. It also includes an exercise in geometry using a clock to understand dividing circles into degrees and naming angles. This system of dividing circles into 360° is an ancient one. A circle of 360 equal parts can be divided into quarter circles (four quadrants) each containing 90 degrees. If using a clock for a model from 12 O'clock to three o'clock is 90 degrees. From 12 O'clock noon to 12 O'clock midnight is 360 degrees.
When students build and use the star plotter in Activity 2, they learn to estimate angles and distances in the sky using their fists. These measurements are not very accurate. To obtain more accurate figures, an instrument may be made to help determine measurements. This is an astrolabe which was invented by the Greeks and disseminated by Islam. This instrument was used to observe and calculate the position of celestial bodies before the invention of the sextant. This activity includes two models, one simple and the other more complicated to measure angles by the stars. It also includes an exercise in geometry using a clock to understand dividing circles into degrees and naming angles. This system of dividing circles into 360° is an ancient one. A circle of 360 equal parts can be divided into quarter circles (four quadrants) each containing 90 degrees. If using a clock for a model from 12 O'clock to three o'clock is 90 degrees. From 12 O'clock noon to 12 O'clock midnight is 360 degrees.
Polaris or the North Star is a place to start measuring the angle above the horizon. This angle is equal to the latitude at the point where the calculation is figured. Latitude refers to the parallel lines which are numbered from the equator at 0 degrees north to the pole (90 degrees north latitude) and south to the opposite pole (90 degrees south latitude). The latitude of the North Star is 90 degrees at the North Pole and overhead there. At the equator, it would be 0 degrees and visible if possible in a direct horizontal position. If one uses the complex astrolabe it is possible to calculate the position of other celestial bodies by comparing them to the position of Polaris. The complex astrolabe will help students to find constellations and make sky maps with the important stars in their correct positions as viewed from a particular latitude. An inexpensive (around $3.00) astrolabe is available from:
Science Kit, Inc. 777 East Park Drive Tonawanda, NY 14150.
Is it helpful to have a system to measure the position of the stars and their height from where we stand? Would it help us to be more accurate in these measurements? How would a measurement made by fists compare numerically with one done by an instrument? How could we check for accuracy of results?
Materials: 8-1/2"x11" sheet of paper or 4' tube; protractor; small weight such as key; thread; tape.
Materials: Protractor; thread; weight; 1" thick wood 6"x 3"; (2) 1/2" thick wood 12' x 1/2'; 1/4" bolt and wing nut; nail; heavy cardboard for 12" circle; straw; glue for metal wood; metal fastener.
Discussion
After many experiences testing this model, students may discuss experiences. In what ways did using this instrument prove helpful? Was it easier to locate constellations with this instrument? Did they record changes in position of stars over a period of hours? Days? What did they discover. How could ancient people learn from this instrument? How could this instrument help us if lost? Is this instrument helpful in making sky maps with the Star plotter?


 Back to Top
Back to Top
 | Home
| Home