EFBe Frame Test: how NOT to test a Bicycle
Engineering for Bikes (EFBe)
performed frame tests on a variety of different bike frames to see
how "strong" (in laymans terms) they are. I first read about this test on
Sheldon Brown's website, where he
provided a copy of the English translation of an article from the EFBe website.
Many people have used this test to draw conclusions regarding regarding
suitability of various materials for bicycle frames. In particular,
since aluminum frames faired better in the tests than steel frames, this
has led many to believe that aluminum is an all-around better frame
material.
Unfortunately, the testing method does not fairly represent real-world
riding stresses on frames, and the conclusions ignore some very basic
information.
The test fixture is designed to mimic riding out of the saddle, which
is generally believed to apply the most stress to a bike frame.
The test applies 268 pounds of force to the cranks for 100,000 cycles,
and then 291 pounds for another 100,000 cycles. The force is applied to
the pedals at an angle that should be consistent with out-of-the-saddle
riding.
Let's suppose that this is a valid test. Their test fixture caused failures
in nine of fourteen frames tested. How could this be?
At a cadence of 60 RPMs, 200,000 cycles is 55 hours of riding. The first
frame failed in under 57,000 cycles -- a good rider at 90 RPMs would reach
this point in about ten and a half hours of riding (out of the saddle).
In real world terms, riders can expect their brand new very expensive
bikes to fail during his first couple of weeks riding in the mountains.
Right away we should know that something is wrong with this test.
About metal fatigue
When you repeatedly apply force to a piece of metal, in general, it will
eventually fail. The higher the force, the fewer cycles to failure, and
the lower the force, the more cycles until failure. However, when the
force falls below a certain threshold, called the endurance limit,
you can repeat the application of force forever, with no failure.
The actual measure for the endurance limit is in stress, not force.
Stress is force per square inch. This means that if something is stressed
above its endurance limit, you can always make it last longer just by
making your metal thicker. You may even make it strong enough that you drive
the stress below the endurance limit, and then it will never fail (under
normal usage).
For aluminum though, the endurance limit is always asumed to be zero (if it is
non-zero, it is too small to be useful). You can never get below the
endurance limit, so
eventually, every aluminum bike frame will fail. The reason consumers
accept this is that (hopefully) aluminum frames are made with the metal
thick enough that the fatigue failure doesn't occur until peak cycles get
up into the hundreds of millions, or higher.
For steel, however, the endurance limit is comfortably distant from zero.
Practical steel supports can be designed that should never fail during
normal operation. The endurance limit for steel typically comes into
play on the order of one million cycles; in other words if something has
survived a million cycles of stress, it should never fail (due to that
level of stress). For a bicycle at a rather slow cadence of 60 RPMs, this
is less than 280 hours of riding.
There are certainly many riders capable of accumulating this many hours
of out-of-the-saddle riding time in a single year, and a few who could
get in a million cycles (out of saddle) in just a couple of months. And
most of these riders have frames which have lasted them much longer than
this. This is simply not the
time scale in which frames should be failing. From this I conclude that
steel-framed bikes are generally designed with all normal usage falling
below the endurance limit.
One of the things this means is that if you do have a steel frame failure, it
is due to one of three things: You exceeded normal usage (e.g. crashed),
or the frame had a manufacturing defect, or the frame was poorly designed.
Note that crashing may not cause immediate failure, but it can lead to
a failure later on. For example,
a crack in a frame will redistribute stress to the areas around the crack.
These areas will see significantly more stress than they saw before there
was a crack, and hence may be prone to an endurance limit failure.
The point to all of this is that they managed to break most frames
(including all of the steel frames), in
far less than a million cycles. This means that somehow, they've subjected
these frames to stresses far in excess of normal riding limits. This
puts any conclusions about frame materials in doubt. Steel frames failed
in the test that may never have failed in real life. Aluminum frames
lasted longer in the test, possibly because they have to be stronger than steel
frames in order to delay their fatigue failure.
Where did they go wrong?
First, lets look at their test setup.
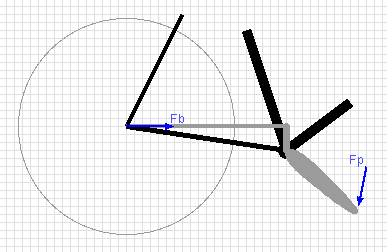 The linkage from
the pedal to rear wheel is approximated by connecting an extension
from the pedal directly to the rear dropout. This applies a force,
Fb as shown in the diagram, directly to the rear dropout. This force exactly
matches the "chain tension" being modelled.
The linkage from
the pedal to rear wheel is approximated by connecting an extension
from the pedal directly to the rear dropout. This applies a force,
Fb as shown in the diagram, directly to the rear dropout. This force exactly
matches the "chain tension" being modelled.
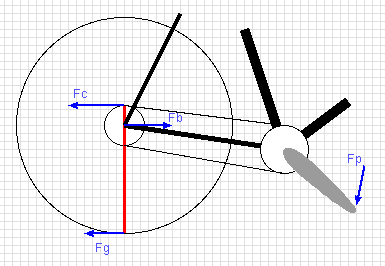 On a real bike, the
chain pulls on the rear wheel, which applies force to the rear dropout
only by levering against the frame from the ground.
This can be modelled as a simple lever arm, shown as the red line
in the diagram. The forces, Fc, Fb, and Fg, are the forces which this
lever applies to the world around it (yes, this is backwards from traditional
free-body diagrams, but I think it is clearer for those with less mechancal
engineering backround, like myself). Fc is the reaction force that the
freewheel cog applies to the chain, as a result of the chain tension.
Fb is the force being applied to the bike at the rear dropout, and Fg is
the force being applied to the ground.
On a real bike, the
chain pulls on the rear wheel, which applies force to the rear dropout
only by levering against the frame from the ground.
This can be modelled as a simple lever arm, shown as the red line
in the diagram. The forces, Fc, Fb, and Fg, are the forces which this
lever applies to the world around it (yes, this is backwards from traditional
free-body diagrams, but I think it is clearer for those with less mechancal
engineering backround, like myself). Fc is the reaction force that the
freewheel cog applies to the chain, as a result of the chain tension.
Fb is the force being applied to the bike at the rear dropout, and Fg is
the force being applied to the ground.
We can calculate the relationship between Fc and Fb, by considering the
torques applied by our red line, around the road contact point. Torques
must balance, so Fc times its distance from the ground must equal
Fb times its distance from the ground. Fb must be a stronger force,
in order to compensate for its shorter torque arm. The difference depends
on the actual sizes. If we assume a 13 inch radius tire, and a big
hill-climbing cog, with a radius of 2.5 inches, then Fc*15.5 must
equal Fb*13, therefore, Fb=1.19*Fc. In other words, the force applied
to the bike is almost 20% higher than that found in the chain.
The EFBe test actually
underestimates the force applied to the dropout by anywhere
from five to twenty percent (depending on the size of the rear cog
being simulated). During
climbing out of the saddle, the rider is more likely on a larger cog, hence
the underestimate is likely closer to twenty percent. Clearly, I'm on the
wrong track here.
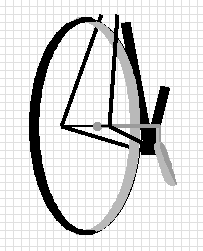
 One area for further analysis is a three-dimensional accounting of all of the
forces. You can get a better view of the linkages in these pictures.
I haven't analyzed these in three dimentions, however it does seem entirely
possible that there will be significant differences in resulting forces,
and especially in torques, because of the differences in where the force
is applied.
It's entirely possible that their linkage can introduce
forces which can't occur in the real world.
One area for further analysis is a three-dimensional accounting of all of the
forces. You can get a better view of the linkages in these pictures.
I haven't analyzed these in three dimentions, however it does seem entirely
possible that there will be significant differences in resulting forces,
and especially in torques, because of the differences in where the force
is applied.
It's entirely possible that their linkage can introduce
forces which can't occur in the real world.
Okay, so the linkage to the rear dropouts
may still be a problem, but to the extent that I'm able
to analyze it, it is actually too gentle. What about the assumptions of
force? Remember, 268 pounds of force, and later 291 pounds.
A top-performing athlete could probably
not achieve these forces for any length of time, because the rider will
probably weigh less than 150 pounds. Such a rider would have to fully unweight
the opposite pedal, and add an addtional 118 (or more, if lighter) pounds of
upward force on the handlebar, for long periods of time.
A heavier rider could more easily
come close to this, although a heavier rider is usually not going to be
fit enough and skilled enough to fully or mostly unweight the opposite
pedal while climbing out of the saddle.
Still, there are a few riders who are heavy, and fit, and have good technique.
So I won't agree that these forces are typical, but I will allow that they
may be attainable by a some small minority of riders.
Still not a slam dunk. It certainly doesn't seem like this should be
enough to account for such a high failure rate.
The big clue to this problem lies with noting that two thirds of the failed
frames failed in the head tube or down tube, even with the force being applied
to the bottom bracket and rear dropouts. How can this be? A close
examination of their test setup reveals what they did wrong: the front fork is
mounted into a rigid fixture.
This introduces forces into the frame which will never be seen on the
road. A bike can never support front-to-back forces at the front fork
dropouts, except under braking or in a collision. Of course, braking
is a tiny percentage
of riding time, and cyclists generally don't continue to pedal out of the
saddle while they brake.
The real-life front forks also only support minimal side-to-side forces,
because the wheel rolls away from any force applied there. The test
fixture can introduce significant side-to-side forces at the front
fork.
It is however a realistic frame test for someone who is going
to bolt their frame into a trainer, and then ride hard on the trainer out of
the saddle for long periods of time. But I think most serious cyclists
who use trainers with fork mounts ought to know that they aren't
supposed to ride them out of the saddle.
It seems likely that this test setup is going to dramatically exceed
design limits around the head tube, which is exactly where most of the
failures occured. And the additional forces introduced at the front
fork would probably have effects throughout the frame, although I haven't
done any sort of analysis to see exactly what these forces might affect.
Conclusions
EFBe offers an approval process where they will put their name on frames
that have passed their tests. They've apparently become quite successful.
This is unfortunate. A frame which has passed their test may well be
weaker in the long run than other frames which failed this test.
This is all particularly frustrating, because they came very close to
doing something really useful. It would be very easy to
fix their testing: redesign the front fork mount; redesign
the linkage to the rear dropout; lower the input forces somewhat;
increase the cycles to a million, before increasing the force.
Instead, all we get is more misinformation, and EFBe gets a nice profit
for it all, too.
Anvil
Bikeworks' article on the EFBe tests.
My Cycling Page
 The linkage from
the pedal to rear wheel is approximated by connecting an extension
from the pedal directly to the rear dropout. This applies a force,
Fb as shown in the diagram, directly to the rear dropout. This force exactly
matches the "chain tension" being modelled.
The linkage from
the pedal to rear wheel is approximated by connecting an extension
from the pedal directly to the rear dropout. This applies a force,
Fb as shown in the diagram, directly to the rear dropout. This force exactly
matches the "chain tension" being modelled.  On a real bike, the
chain pulls on the rear wheel, which applies force to the rear dropout
only by levering against the frame from the ground.
This can be modelled as a simple lever arm, shown as the red line
in the diagram. The forces, Fc, Fb, and Fg, are the forces which this
lever applies to the world around it (yes, this is backwards from traditional
free-body diagrams, but I think it is clearer for those with less mechancal
engineering backround, like myself). Fc is the reaction force that the
freewheel cog applies to the chain, as a result of the chain tension.
Fb is the force being applied to the bike at the rear dropout, and Fg is
the force being applied to the ground.
On a real bike, the
chain pulls on the rear wheel, which applies force to the rear dropout
only by levering against the frame from the ground.
This can be modelled as a simple lever arm, shown as the red line
in the diagram. The forces, Fc, Fb, and Fg, are the forces which this
lever applies to the world around it (yes, this is backwards from traditional
free-body diagrams, but I think it is clearer for those with less mechancal
engineering backround, like myself). Fc is the reaction force that the
freewheel cog applies to the chain, as a result of the chain tension.
Fb is the force being applied to the bike at the rear dropout, and Fg is
the force being applied to the ground.
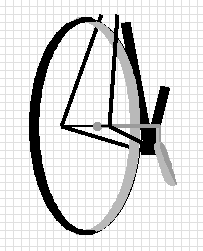
 One area for further analysis is a three-dimensional accounting of all of the
forces. You can get a better view of the linkages in these pictures.
I haven't analyzed these in three dimentions, however it does seem entirely
possible that there will be significant differences in resulting forces,
and especially in torques, because of the differences in where the force
is applied.
It's entirely possible that their linkage can introduce
forces which can't occur in the real world.
One area for further analysis is a three-dimensional accounting of all of the
forces. You can get a better view of the linkages in these pictures.
I haven't analyzed these in three dimentions, however it does seem entirely
possible that there will be significant differences in resulting forces,
and especially in torques, because of the differences in where the force
is applied.
It's entirely possible that their linkage can introduce
forces which can't occur in the real world.
 Fine's Home
Fine's Home