Poisson vs Gaussian, Part 2
Probability density functions are another way of summarizing the consequences of assuming a Gaussian error distribution when the true distribution is Poisson. We can compute the posterior probability of the intensity of a source, when some number of counts are observed in a source region, and the background is estimated using counts observed in a different region. We can then compare it to the equivalent Gaussian.
The figure below (AAS 472.09) compares the pdfs for the Poisson intensity (red curves) and the Gaussian equivalent (black curves) for two cases: when the number of counts in the source region is 50 (top) and 8 (bottom) respectively. In both cases a background of 200 counts collected in an area 40x the source area is used. The hatched region represents the 68% equal-tailed interval for the Poisson case, and the solid horizontal line is the ±1σ width of the equivalent Gaussian.
Clearly, for small counts, the support of the Poisson distribution is bounded below at zero, but that of the Gaussian is not. This introduces a visibly large bias in the interval coverage as well as in the normalization properties. Even at high counts, the Poisson is skewed such that larger values are slightly more likely to occur by chance than in the Gaussian case. This skew can be quite critical for marginal results.
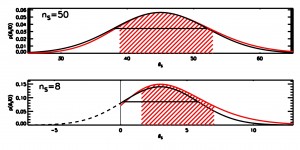
Poisson and Gaussian probability densities
No simple IDL code this time; but for reference, the Poisson posterior probability density curves were generated with the PINTofALE routine ppd_src()
hlee:
The first sentence, because of “probability density function,” sounds self contradictory to me. If it’s replaced by “empirical distribution function” it seems o.k. but I’m a bit cautious to assure it since I couldn’t find literature in astronomy that used “empirical cdf.” I’ll get back to the issue why I felt uncomfortable with the first sentence later in my [MADS]. I just wanted to let astronomers know Berry–Esséen theorem (wiki link). A brief self defense for the uncomfortable feeling is that Poisson and Gaussian both has its own probability density function, which belongs to an exponential family and I guess F_n(x) in the Berry-Esseen is related to your “probability density function.”
04-15-2009, 12:33 amvlk:
It’s just the pdf, the joint posterior of source and background marginalized over background. What’s contradictory about it?
04-15-2009, 5:33 amhlee:
As I kept confused with astronomer’s “model uncertainty” although I know it is used differently from statistician’s “model uncertainty”, perhaps pdf is one of such. Poisson pdf and Gaussian pdf have their own equation formats, so in probability Poisson pdf cannot be written in terms of Gaussian pdf; however, in distribution, asymptotically via joint distributions or likelihoods (not a function of single datum X, but a function of X_1,…,X_n), as if done with the central limit theorem, the empirical distribution of Poisson data can be represented by Normal distribution. I read the first sentence as “A pdf (a equation of a certain class, defined on the space of positive integers) is summarized by the other equation (Gaussian pdf, symmetric, spans from -infty to infty)” when a Poisson pdf is not comparable to a normal pdf.
The reason of introducing the Berry-Esseen is that it proves such gap is inevitable in approximation (doesn’t matter whether a sampling distribution is Poisson, Gamma, binomial, etc) and it tells that there’s lower bound in gaps although case by case the gap sizes would be different let alone sample sizes. One would surprise how large n can be in order to make the gap small enough to a tolerable level. Note that it assumes iid and poses some constraints on moments. Theorems are there to be modified by relaxing conditions and assumptions, say from iid to independent, to prove other problems. Such tailoring yields a new theorem with another name or corollaries. Instead of saying >25 is a golden absolute rule and 10> is wrong in X-ray spectral grouping (counts in bins), I’d like to say more care is needed when data are binned/grouped. It’s hard to know those counts in each group satisfy these assumptions and produce small enough gap of tolerance for traditional the x-sigma error bar construction based on the delta chi method.
Fortunately, there are many efforts to minimize the impact of gaps in your plots with low count data while lessening sacrifice of innate information. They look so far just rules of thumb without mathematical justifications; at least documentations from XSPEC and Sherpa gave me such impression (some literatures take 20 intead of 25, suggest averaging errors of neighbors but do not provide definition/function/explanation to define degrees of neighborhood, etc). Quite room for mathematical statisticians to accompany astronomers’ lonely quest and to guide as well.
04-15-2009, 2:33 pmvlk:
I’m afraid you are reading too much into it. Given data in the form of counts, you can calculate the exact posterior pdf for the source intensity based on the Poisson likelihood. That gives one curve. You can also make an approximation and compute the equivalent Gaussian MLE and variance. That gives another curve. Compare, contrast, conclude.
04-15-2009, 4:31 pm