different views
An email was forwarded with questions related to the data sets found in “Be an INTEGRAL astronomer”. Among the sets, the following scatter plot is based on the Crab data.
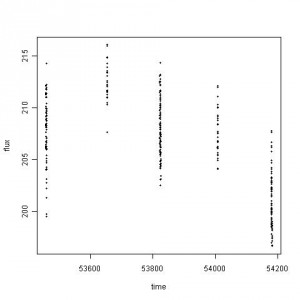 |
If you do not mind the time predictor, it is hard to believe that this is a light curve, time dependent data. At a glance, this data set represents a simple block design for the one-way ANOVA. ANOVA stands for Analysis of Variance, which is not a familiar nomenclature for astronomers.
Consider a case that you have a very long strip of land that experienced FIVE different geological phenomena. What you want to prove is that crop productivity of each piece of land is different. So, you make FIVE beds and plant same kind seeds. You measure the location of each seed from the origin. Each bed has some dozens of seeds, which are very close to each other but their distances are different. On the other hand, the distance between planting beds are quite far unable to say that plants in the test bed A affects plants in B. In other words, A and B are independent suiting for my statistical inference procedure by the F-test. All you need is after a few months, measuring the total weight of crop yield from each plant (with measurement errors).
Now, let’s look at the plot above. If you replace distance to time and weight to flux, the pattern in data collection and its statistical inference procedure matches with the one-way ANOVA. It’s hard to say this data set is designed for time series analysis apart from the complication in statistical inference due to measurement errors. How to design the statistical study with measurement errors, huge gaps in time, and unequal time intervals is complex and unexplored. It depends highly on the choice of inference methods, assumptions on error i.e. likelihood function construction, prior selection, and distribution family properties.
Speaking of ANOVA, using the F-test means that we assume residuals are Gaussian from which one can comfortably modify the model with additive measurement errors. Here I assume there’s no correlation in measurement errors and plant beds. How to parameterize the measurement errors into model depends on such assumptions as well as how to assess sampling distribution and test statistics.
Although I know this Crab nebula data set is not for the one-way ANOVA, the pattern in the scatter plot drove me to test the data set. The output said to reject the null hypothesis of statistically equivalent flux in FIVE time blocks. The following is R output without measurement errors.
Df Sum Sq Mean Sq F value Pr(>F)
factor 4 4041.8 1010.4 143.53 < 2.2e-16 ***
Residuals 329 2316.2 7.0
If the gaps are minor, I would consider time series with missing data next. However, the missing pattern does not agree with my knowledge in missing data analysis. I wonder how astronomers handle such big gaps in time series data, what assumptions they would take to get a best fit and its error bar, how the measurement errors are incorporated into statistical model, what is the objective of statistical inference, how to relate physical meanings to statistical significant parameter estimates, how to assess the model choice is proper, and more questions. When the contest is over, if available, I’d like to check out any statistical treatments to answer these questions. I hope there are scientists who consider similar statistical issues in these data sets by the INTEGRAL team.
Leave a comment