Last modified: February 26, 2007
This thread uses PINTofALE to generate a simulated Chandra spectrum. The Chandra ARF and RMF used were obtained from the Chandra Proposal Information page and placed in !ARDB. Here, we will generate an ACIS-I spectrum for a star that has a nominal ROSAT/PSPC count-rate of 0.1 ct/s (you must have PIMMS installed locally to do this). The steps involved are:
# start IDL
idl
; set up the PoA environment ;
.run initale
;NOTE:
; if INITALE fails, run the script
; @PoA_constructor
; Change some of the preset defaults to values reasonable
; for this exercize
!LDBDIR='$SPEX'
;Warning: APED emissivities include ion balance from
;Mazzotta et al., and abundances from Anders & Grevesse.
;Care must be taken to not include them twice:
if strpos(strlowcase(!LDBDIR),'aped',0) ge 0 then !IONEQF='none'
if strpos(strlowcase(!LDBDIR),'aped',0) ge 0 then $
!ABUND = !ABUND/getabund('anders & grevesse')
!NH=3e20
; A Differential Emission Measure (DEM) is required to estimate
; the amount of emission at any given temperature. Typically
; a 2-temperature model is used, as in the example below:
!DEM = mk_dem('delta', logT=!LOGT, pardem=alog10([7.55e6, 23.4e6]),$
indem=[5.1d12,6.1d12]*0.05)
; NOTE: the above is the only option available in the
; chandra_acis_ao7.par file.
; In general, stellar coronal plasmas are characterized by a
; multi-temperature emission measure. It is possible to
; define a DEM from scratch interactively, using MK_DEM
; (left click to define points along a DEM curve, and
; right click to exit)
;
!DEM = mk_dem('cursor', logT=!LOGT, pardem=[1e10,1e14], $
xcur=mk_dem_xcur, ycur=mk_dem_ycur)
; A DEM thus derived may be edited in detail with DEMACS
;
!DEM = demacs(!LOGT, DEM0=!DEM, logT0=!LOGT, group=group, igroup=igroup)
; more complicated DEMs, (e.g., splines) may also be defined:
;
in_pardem=[3.00000,4.01421,5.35229,5.49464,6.46261,7.06759,7.40923]
in_indem=[500.050,188.068,2.71397,2.16901,159.778,24.0164,0.133006]*1e11
!DEM = mk_dem('spline', logT=!LOGT, indem=in_indem, pardem=in_pardem) > 0
; for the sake of definiteness, we will use a 2-temperature
; delta-function emission measure distribution in the following
; example.
T_components = [6.9, 7.4] ;log(T[K]) components in the EM
EM_components = [5.1d12, 6.1d12] ;Emission Measure [cm^-3]
!DEM=mk_dem('delta',logT=!LOGT,pardem=T_components,indem=EM_components)
plot,!logT,!DEM,xtitle='log!d10!n(T [K])',ytitle='DEM [cm!u-5!n/logK]'
;NOTE:
; this is a completely arbitrary DEM(T), and its only saving
; grace is that it looks sensible. It definitely would not
; generate the correct number of ROSAT counts and must be
; renormalized.
; We will assume that a ROSAT/PSPC count rate is available,
; and that the simulation will match this rate. Data from
; other missions such as ASCA, BeppoSAX, etc. can be dealt
; with in the same manner.
; First find and read in the ROSAT/PSPC effective area
; you will need to know where your local PIMMS installation
; is to do this.
;
pimmsdir = '/soft/pimms/data' ;<<<change to your local installation
rosat_pspc_open = get_pimms_file('ROSAT','PSPC','OPEN',pdir=pimmsdir)
;
rd_pimms_file, rosat_pspc_open, pspc_effar, pspc_wvlar, /wave
; make sure that the wavelengths are sorted in increasing order
;
ae=sort(pspc_wvlar) & pspc_wvlar=pspc_wvlar[ae] & pspc_effar=pspc_effar[ae]
; some initializations
;
src_DIST=10. ;place the source (say) 10 pc away
; the DEM needed for the script MAKE_SPECTRUM (which will
; be called below) must be the DEM defined at the source
; (distance will be corrected for within the script). Hence,
; rescale the currently defined DEM (which has reasonable
; values for a DEM "at Earth").
;
src_DCOR = 10.D^(alog10(4.*!DPI)+2.*alog10(src_DIST*3.1d18))
!DEM = !DEM * src_DCOR
; now make a ROSAT/PSPC spectrum using MAKE_SPECTRUM,
; which is a script and requires that its inputs be
; in specially named variables and have the correct
; units. A more flexible approach is outlined in the
; example sessions.
;
v_LOGT=!LOGT ;temperature grid
v_DEM=!DEM ;DEM in [cm^-3]
v_DIST=src_DIST ;distance in [pc]
v_EFFAR=pspc_effar > 0 ;effective area in [cm^2]
v_WVLAR=pspc_wvlar ;effective area wavelength grid in [Ang]
v_WGRID=mid2bound(pspc_wvlar) ;sorted wavelength bin boundaries in [Ang]
v_EXPTIME=50. ;nominal exposure time [ks] (say)
v_RMF='none' ;name of OGIP-compatible RMF
;
;NOTE:
; note that convolving with an RMF is unnecessary at this stage
; because all we need is a total count rate estimate
;
.run make_spectrum
; get the total count-rate and normalize the DEM to the
; "observed" rate of 0.1 ct/s
;
obs_rate = 0.1 ;[ct/s]
pred_rate = total(v_flxspc/v_EXPTIME/1e3) ;[ct/s]
print,'normalization factor: ',obs_rate/pred_rate
;normalization factor: 0.0030849559
!DEM = !DEM * obs_rate/pred_rate
; first read in the Chandra ACIS-I on-axis ARF ; acisi_effar=rdarf(!ARDB+'/acisi_aimpt_cy07.arf',arstr) ; figure out the spectral binning required ; elo=arstr.ELO & ehi=arstr.EHI & wlo=12.3985/ehi & whi=12.3985/elo ; now reverse such that wavelengths are in increasing order ; wlo=reverse(wlo) & whi=reverse(whi) & acisi_effar=reverse(acisi_effar) wgrid=[wlo,max(whi)] & midwvl=0.5*(wgrid+wgrid[1:*]) ; set up to call MAKE_SPECTRUM again ; v_LOGT=!LOGT ;temperature grid v_DEM=!DEM ;DEM in [cm^-3] v_EFFAR=acisi_effar ;effective area in [cm^2] v_WVLAR=midwvl ;effective area wavelength grid in [Ang] v_WGRID=wgrid ;sorted wavelength bin boundaries in [Ang] v_EXPTIME=50. ;nominal exposure time [ks] v_RMF=!ARDB+'/acisi_aimpt_cy07.rmf' ;name of OGIP-compatible RMF ; and make the observed counts spectrum ; .run make_spectrum ; simulate an actual observation by finding Poisson deviates ; nbin=n_elements(v_CTSPC) sim_spec=intarr(nbin) for i=0L,nbin-1L do $ if v_CTSPC[i] gt 0 then sim_spec[i]=randomu(seed,poisson=v_CTSPC[i]) ; plot ; plot,v_CHAN,v_CTSPC,xtitle='[keV]',ytitle='[ct]',/xl,xr=[0.5,7],$ /yl,yr=[0.1,300],thick=2 oplot,v_CHAN,sim_spec,psym=10,thick=2,color=3
; First note that the above results are consistent with rough
; PIMMS results. For a ROSAT/PSPC count rate of 0.1 ct/s,
; a Raymond-Smith spectrum of temperature 0.54 keV produces
; approx 0.14 ct/s with Chandra/ACIS-I. This is within a
; factor of 2 of the value predicted here:
;
print,total(v_CTSPC)/v_EXPTIME/1e3
; 0.174697957
; MARX requires a spectrum in an ASCII file of 2 columns,
; with column 1 containing the energy grid in [keV] and
; column 2 containing the flux density in [ph/s/cm^2/keV]
; Now, v_LINSPC[v_WVLS] and v_CONSPC[v_WVLS] are already
; almost in this form. They must be converted from
; [ph/s/cm^2/bin] to [ph/s/cm^2/keV]. A point to note is
; that v_WVLS was derived within MAKE_SPECTRUM as the
; mid-bin value of the bin boundaries in v_WGRID.
; convert from [Ang] to [keV]
;
v_ENERGY=12.3985/v_WVLS
Egrid=12.3985/v_WGRID
; and get the bin width
;
dE=abs(Egrid[1:*]-Egrid)
; derive MARX compatible flux density
;
spec_MARX = (v_LINSPC + v_CONSPC) / dE
; reverse the arrays (so that they are in increasing order of energy)
;
spec_MARX = reverse(spec_MARX)
v_ENERGY = reverse(v_ENERGY)
; and print out to file
;
openw,umarx,'spec_marx.dat',/get_lun
for i=0L,n_elements(v_ENERGY)-1L do printf,umarx,v_ENERGY[i],spec_MARX[i]
close,umarx & free_lun,umarx
; see the MARX manual at http://space.mit.edu/ASC/MARX/
; for details on how to obtain and run MARX. Note that updating
; to MARX 4.2.0 will allow for for Cycle 7 simulations including ACIS
; contamination (this will be necessary to match the ARF used in this
; example).
;
; We have run MARX independently on the spectrum written out
; above, using the recipe prescribed in section 5 of the manual.
;
; cp /soft/marx/marx.par .
; pset marx.par ExposureTime=50000 OutputDir='sim_marx' \
; GratingType='NONE' DetectorType='ACIS-I' SourceFlux=-1 \
; SpectrumType='FILE' SpectrumFile='spec_marx.dat' \
; SourceType='POINT' DitherModel='INTERNAL'
; marx TSTART=2006.46
; marx2fits sim_marx/ spec_marx.evt
; dmextract infile="spec_marx.evt[EVENTS][(x,y)=circle(4018,4141,10)]
; [bin pi=1:1024:1]" outfile="spec_marx.pi" clobber=yes verbose=2
; now read in the binned spectrum from the MARX simulation
M_CTSPC=mrdfits('spec_marx.pi',1,hdr)
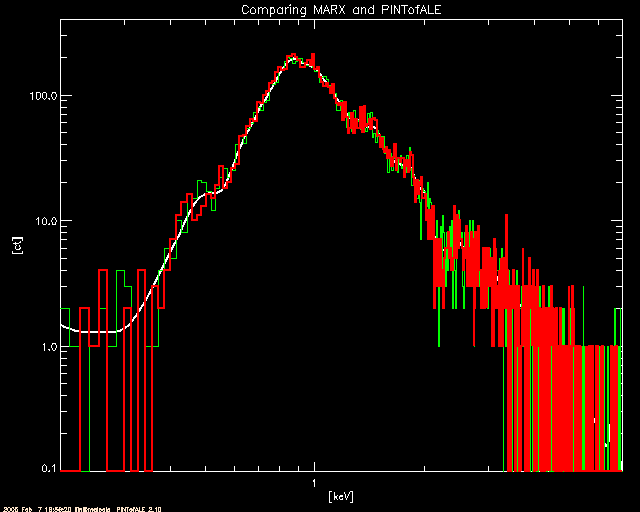
; and overplot (in red) on the PINTofALE simulation (green)
; (note that we do not expect perfect agreement because we have
; used a very rough ARF in section 3 above. nevertheless, the
; agreement is good.)
;
plot,v_CHAN,v_CTSPC,/xl,xr=[0.2,7],/xs,/yl,yr=[0.1,400],/ys,thick=2,$
xtitle='[keV]',ytitle='[ct]',title='Comparing MARX and PINTofALE'
oplot,v_CHAN,sim_spec,psym=10,color=3
oplot,v_CHAN,M_CTSPC.COUNTS,psym=10,thick=2,color=2
